/Szkoła średnia/Zadania maturalne/Matura 2020/Matura
Egzamin Maturalny
z Matematyki poziom rozszerzony 15 czerwca 2020 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 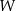 określony wzorem
określony wzorem 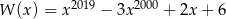
A) jest podzielny przez 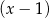 i z dzielenia przez
i z dzielenia przez 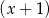 daje resztę równą 6.
daje resztę równą 6.
B) jest podzielny przez 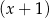 i z dzielenia przez
i z dzielenia przez 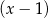 daje resztę równą 6.
daje resztę równą 6.
C) jest podzielny przez 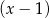 i jest podzielny przez
i jest podzielny przez 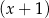 .
.
D) nie jest podzielny ani przez 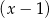 , ani przez
, ani przez 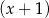 .
.
Ciąg 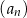 jest określony wzorem
jest określony wzorem 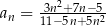 dla każdej liczby
dla każdej liczby 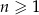 . Granica tego ciągu jest równa
. Granica tego ciągu jest równa
A) 3 B) 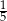 C)
C)  D)
D) 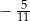
Mamy dwie urny. W pierwszej są 3 kule białe i 7 kul czarnych, w drugiej jest jedna kula biała i 9 kul czarnych. Rzucamy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek, od jednego oczka do sześciu oczek. Jeśli w wyniku rzutu otrzymamy ściankę z jednym oczkiem, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – losujemy jedną kulę z drugiej urny. Wtedy prawdopodobieństwo wylosowania kuli białej jest równe
A) 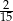 B)
B) 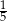 C)
C)  D)
D) 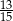
Po przekształceniu wyrażenia algebraicznego 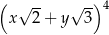 do postaci
do postaci 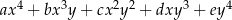 współczynnik
współczynnik  jest równy
jest równy
A) 6 B) 36 C) 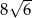 D)
D) 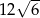
Zadania otwarte
W trójkącie 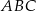 bok
bok 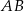 jest 3 razy dłuższy od boku
jest 3 razy dłuższy od boku 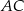 , a długość boku
, a długość boku 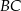 stanowi
stanowi 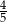 długości boku
długości boku 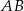 . Oblicz cosinus najmniejszego kąta trójkąta
. Oblicz cosinus najmniejszego kąta trójkąta 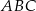 .
.
Wyznacz wszystkie wartości parametru  , dla których równanie
, dla których równanie 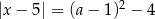 ma dwa różne rozwiązania dodatnie.
ma dwa różne rozwiązania dodatnie.
Dany jest trójkąt równoramienny 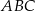 , w którym
, w którym 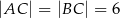 , a punkt
, a punkt 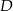 jest środkiem podstawy
jest środkiem podstawy 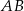 . Okrąg o środku
. Okrąg o środku 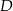 jest styczny do prostej
jest styczny do prostej 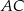 w punkcie
w punkcie 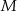 . Punkt
. Punkt 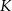 leży na boku
leży na boku 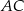 , punkt
, punkt 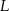 leży na boku
leży na boku 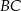 , odcinek
, odcinek 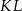 jest styczny do rozważanego okręgu oraz
jest styczny do rozważanego okręgu oraz 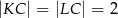 (zobacz rysunek).
(zobacz rysunek).
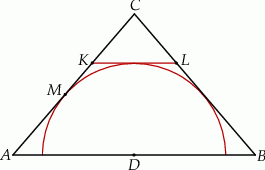
Wykaż, że 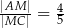 .
.
Liczby dodatnie  i
i 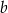 spełniają równość
spełniają równość 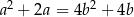 . Wykaż, że
. Wykaż, że 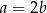 .
.
Rozwiąż równanie 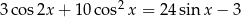 dla
dla 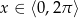 .
.
W trzywyrazowym ciągu geometrycznym 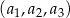 spełniona jest równość
spełniona jest równość 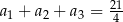 . Wyrazy
. Wyrazy 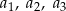 są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz
są – odpowiednio – czwartym, drugim i pierwszym wyrazem rosnącego ciągu arytmetycznego. Oblicz 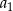 .
.
Dane jest równanie kwadratowe 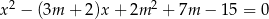 z niewiadomą
z niewiadomą  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 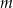 , dla których różne rozwiązania
, dla których różne rozwiązania 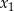 i
i 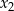 tego równania istnieją i spełniają warunek
tego równania istnieją i spełniają warunek
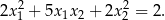
Prosta o równaniu 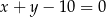 przecina okrąg o równaniu
przecina okrąg o równaniu 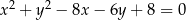 w punktach
w punktach 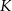 i
i 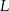 . Punkt
. Punkt 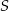 jest środkiem cięciwy
jest środkiem cięciwy 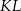 . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku 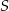 i skali
i skali 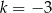 .
.
Oblicz, ile jest wszystkich siedmiocyfrowych liczb naturalnych, w których zapisie dziesiętnym występują dokładnie trzy cyfry 1 i dokładnie dwie cyfry 2.
Podstawą ostrosłupa czworokątnego 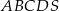 jest trapez
jest trapez 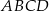 (
(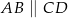 ). Ramiona tego trapezu mają długości
). Ramiona tego trapezu mają długości 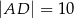 i
i 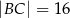 , a miara kąta
, a miara kąta 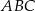 jest równa
jest równa 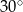 . Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt
. Każda ściana boczna tego ostrosłupa tworzy z płaszczyzną podstawy kąt  , taki, że
, taki, że 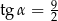 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
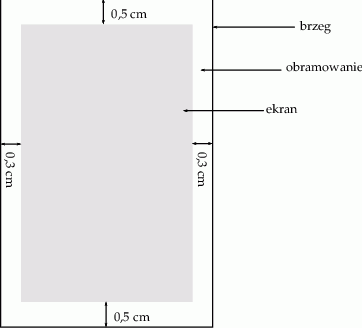
Należy zaprojektować wymiary prostokątnego ekranu smartfona, tak aby odległości tego ekranu od krótszych brzegów smartfona były równe 0,5 cm każda, a odległości tego ekranu od dłuższych brzegów smartfona były równe 0,3 cm każda (zobacz rysunek – ekran zaznaczono kolorem szarym). Sam ekran ma mieć powierzchnię 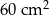 . Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.
. Wyznacz takie wymiary ekranu smartfona, przy których powierzchnia ekranu wraz z obramowaniem jest najmniejsza.