/Szkoła średnia

Zadanie nr 1313013

Dodaj do ulubionych
Dodaj do rozwiązanych

W czworościanie, którego wszystkie krawędzie mają taką samą długość 6, umieszczono kulę tak, że ma ona dokładnie jeden punkt wspólny z każdą ścianą czworościanu. Płaszczyzna 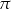π , równoległa do podstawy tego czworościanu, dzieli go na dwie bryły: ostrosłup o objętości równej 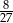-8 27 objętości dzielonego czworościanu i ostrosłup ścięty. Oblicz odległość środka 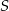S kuli od płaszczyzny 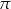π , tj. długość najkrótszego spośród odcinków 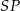SP , gdzie 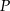P jest punktem płaszczyzny π .

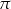Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

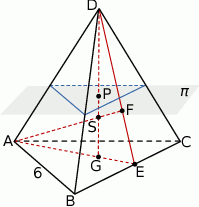
Rozpocznijmy od obliczenia długości wysokości 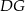DG czworościanu oraz promienia 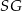SG kuli wpisanej w ten czworościan.

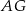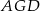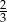Przyprostokątna AG trójkąta prostokątnego AGD to 2 3 wysokości 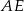AE trójkąta równobocznego 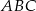ABC , więc

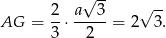
-- 2 a√ 3 √ -- AG = -⋅ -----= 2 3. 3 2

Stąd

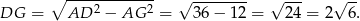
∘ ----2-------2 √ -------- √ --- √ -- DG = AD − AG = 36− 12 = 24 = 2 6.

Korzystamy teraz z podobieństwa trójkątów prostokątnych 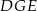DGE i DF S .

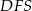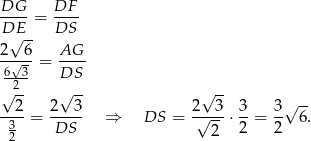
DG DF ----= ---- DE√ -- DS 2 6 AG 6√-3-= DS-- --2- √ 2- 2√ 3- 2√ 3- 3 3 √ -- ----= ----- ⇒ DS = -√---⋅--= -- 6. 32 DS 2 2 2

Wiemy, że objętość czworościanu odciętego płaszczyzną 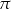π stanowi

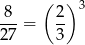
( ) 3 -8-= 2- 27 3

objętości całego czworościanu, więc ten mniejszy czworościan jest podobny do czworościanu 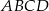ABCD w skali 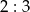2 : 3 . W szczególności

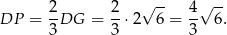
2- 2- √ -- 4-√ -- DP = 3 DG = 3 ⋅ 2 6 = 3 6.

Stąd

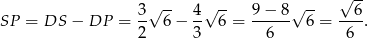
√ -- 3√ -- 4-√ -- 9-−-8-√ -- --6- SP = DS − DP = 2 6 − 3 6 = 6 6 = 6 .

 
Odpowiedź: √ - SP = --6 6

Wersja PDF