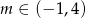Zadanie nr 1374422
Wyznacz wszystkie wartości parametru 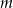 , dla których równanie
, dla których równanie 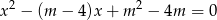 ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od
ma dwa różne pierwiastki rzeczywiste, których suma jest mniejsza od 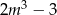 .
.
Rozwiązanie
Sprawdźmy najpierw, kiedy równanie ma dwa różne pierwiastki rzeczywiste.
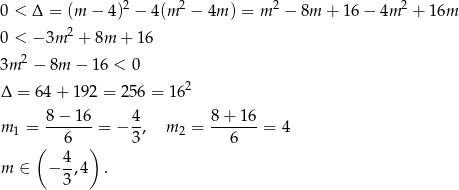
Na mocy wzorów Viète’a wiemy, że suma pierwiastków równania jest równa
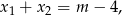
co daje nierówność
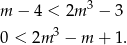
Widać, że prawa strona zeruje się dla 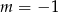 (sprawdzamy dzielniki wyrazu wolnego), dzielimy więc prawą stronę przez
(sprawdzamy dzielniki wyrazu wolnego), dzielimy więc prawą stronę przez 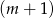 – my zrobimy to grupując wyrazy.
– my zrobimy to grupując wyrazy.
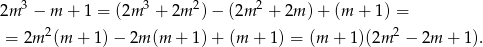
Trójmian w nawiasie jest zawsze dodatni (bo 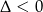 ), więc rozwiązaniem nierówności
), więc rozwiązaniem nierówności
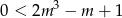
jest przedział 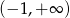 . Uwzględniając warunek z
. Uwzględniając warunek z 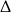 -ą mamy
-ą mamy
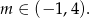
Odpowiedź: