/Szkoła średnia

Zadanie nr 1554344

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż nierówność 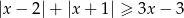|x − 2|+ |x + 1 | ≥ 3x − 3 .

Rozwiązanie

Żeby móc opuścić wartości bezwzględne rozważymy 3 przypadki.

Jeżeli 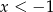x < − 1 to wyrażenia pod obydwiema wartościami bezwzględnymi są ujemne i mamy nierówność

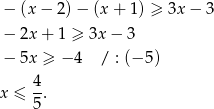
− (x − 2) − (x + 1) ≥ 3x − 3 − 2x + 1 ≥ 3x− 3 − 5x ≥ − 4 / : (− 5) 4 x ≤ -. 5

Czyli w tym przypadku otrzymujemy przedział 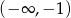(− ∞ ,− 1) .

Jeżeli 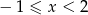− 1 ≤ x < 2 to mamy nierówność

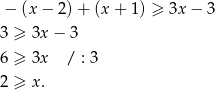
− (x − 2) + (x + 1) ≥ 3x − 3 3 ≥ 3x− 3 6 ≥ 3x / : 3 2 ≥ x.

co daje przedział rozwiązań 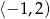⟨− 1 ,2 ) .

Jeżeli natomiast 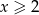x ≥ 2 to wyrażenia pod obydwiema wartościami bezwzględnymi są dodatnie i mamy nierówność

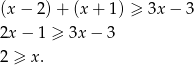
(x− 2)+ (x+ 1) ≥ 3x − 3 2x − 1 ≥ 3x − 3 2 ≥ x.

Zatem w tym przypadku jedynym rozwiązaniem jest 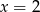x = 2 .

Ostatecznie rozwiązaniem nierówności jest przedział 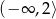(− ∞ ,2⟩ .  
Odpowiedź: (− ∞ ,2⟩

Wersja PDF