/Szkoła średnia

Zadanie nr 1694387

Dodaj do ulubionych
Dodaj do rozwiązanych

Pierwiastkami wielomianu stopnia trzeciego są liczby 1, 3, 5. Współczynnik przy najwyższej potędze zmiennej tego wielomianu jest równy 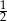12 . Uzasadnij, że dla każdej liczby całkowitej nieparzystej wartość tego wielomianu jest liczbą podzielną przez 24.

Rozwiązanie

Z podanych informacji wiemy, że wielomian ma postać

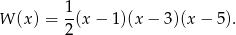
1 W (x) = -(x − 1)(x − 3)(x − 5 ). 2

Jeżeli 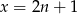x = 2n + 1 jest liczbą całkowitą nieparzystą to mamy

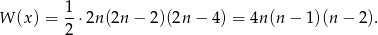
1 W (x ) = --⋅2n(2n − 2)(2n − 4) = 4n (n − 1)(n − 2). 2

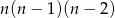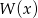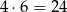Liczba n(n − 1 )(n− 2) jako iloczyn trzech kolejnych liczb całkowitych jest parzysta i dzieli się przez 3, więc jest podzielna przez 6. W takim razie W (x) dzieli się przez 4 ⋅6 = 24 .

Wersja PDF