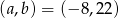/Szkoła średnia

Zadanie nr 1901036

Dodaj do ulubionych
Dodaj do rozwiązanych

Wielomian 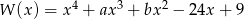4 3 2 W (x) = x + ax + bx − 24x + 9 jest kwadratem wielomianu 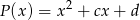P (x) = x2 + cx + d . Oblicz a oraz b .

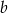Rozwiązanie

Podnieśmy wielomian 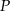P do kwadratu.

2 2 2 4 2 2 2 3 2 [P(x)] = (x + cx + d) = x + cx + d + 2cx + 2dx + 2cdx.

Mamy zatem równanie

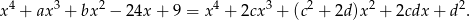
x4 + ax3 + bx2 − 24x + 9 = x4 + 2cx3 + (c2 + 2d)x2 + 2cdx + d 2.

Jeżeli wielomiany są równe to muszą mieć równe współczynniki przy odpowiednich potęgach x -a, co prowadzi do układu równań

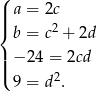
( || a = 2c |{ b = c2 + 2d ||| − 24 = 2cd ( 9 = d2.

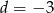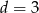Ostatnie równanie oznacza, że d = − 3 lub d = 3 . Trzecie równanie układu przyjmuje wtedy odpowiednio postać

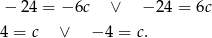
− 24 = − 6c ∨ − 24 = 6c 4 = c ∨ − 4 = c.

Z pierwszego równania układu mamy wtedy odpowiednio

a = 8 ∨ a = −8 .

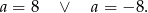
Z drugiego równania mamy

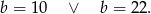
b = 10 ∨ b = 22.

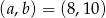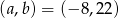Otrzymaliśmy więc dwa rozwiązania (a,b ) = (8,10) lub (a,b) = (− 8,22) .  
Odpowiedź: 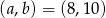(a,b) = (8,10) lub (a,b) = (−8 ,22)

Wersja PDF