/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 9 maja 2020 Czas pracy: 180 minut
Zadania zamknięte
Liczba punktów wspólnych wykresów funkcji 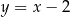 i
i 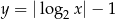 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba 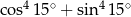 jest równa
jest równa
A) 1 B)  C)
C) 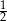 D)
D) 
Na rysunku przedstawiono fragment wykresu pochodnej 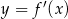 funkcji
funkcji 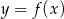 .
.
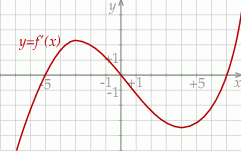
Wynika stąd, że
A) 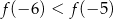 B)
B) 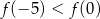 C)
C) 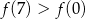 D)
D) 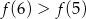
Z talii 52 kart wylosowano jedną kartę. Jakie jest prawdopodobieństwo, że wylosowano damę jeżeli wiadomo, że wylosowana karta nie jest ani kierem ani królem?
A) 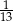 B)
B) 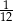 C)
C) 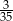 D)
D) 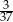
Zadania otwarte
Uzasadnij, że 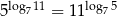 .
.
Oblicz granicę 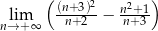 .
.
Zbiór 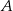 ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór
ma tę własność, że poprzez usuwanie z niego jednego lub dwóch elementów można utworzyć 190 różnych zbiorów. Ile elementów ma zbiór 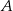 ?
?
Wyznacz równanie stycznej do wykresu funkcji 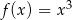 , która przecina oś
, która przecina oś 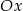 w jednym punkcie:
w jednym punkcie: 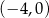 .
.
Wykaż, że jeżeli 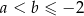 , to
, to 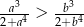 .
.
Na bokach 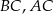 i
i 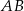 trójkąta
trójkąta 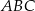 wybrano odpowiednio punkty
wybrano odpowiednio punkty 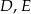 i
i 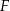 . Wykaż, że jeżeli okręgi opisane na trójkątach
. Wykaż, że jeżeli okręgi opisane na trójkątach 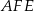 i
i 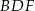 są styczne, to punkt
są styczne, to punkt 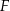 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 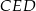 .
.
Przekątna 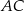 równoległoboku
równoległoboku 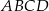 tworzy z jego bokami kąty o miarach
tworzy z jego bokami kąty o miarach 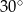 i
i 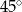 . Oblicz stosunek
. Oblicz stosunek 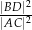 kwadratów długości przekątnych tego równoległoboku.
kwadratów długości przekątnych tego równoległoboku.
Punkt 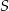 jest punktem przecięcia się przekątnych równoległoboku
jest punktem przecięcia się przekątnych równoległoboku 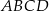 , a punkt
, a punkt 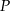 jest takim punktem boku
jest takim punktem boku 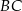 tego równoległoboku, że
tego równoległoboku, że 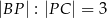 . Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka
. Oblicz współrzędne spodka wysokości opuszczonej z wierzchołka 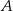 tego równoległoboku na prostą
tego równoległoboku na prostą 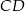 , jeżeli
, jeżeli ![−→ AB = [4,4]](https://img.zadania.info/zes/0047082/HzesT47x.gif) ,
, ![−→ DS = [3 ,− 3]](https://img.zadania.info/zes/0047082/HzesT48x.gif) i
i 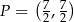 .
.
Dany jest nieskończony ciąg geometryczny 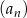 , który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym
, który zawiera zarówno wyrazy dodatnie, jak i ujemne, w którym 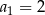 , oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu
, oraz drugi, czwarty i piąty wyraz są kolejnymi wyrazami ciągu arytmetycznego. Wykaż, że suma sześcianów wszystkich wyrazów ciągu 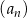 jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
jest równa sumie kwadratów wszystkich wyrazów tego ciągu.
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie
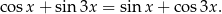
Wykaż, że dla dowolnej liczby rzeczywistej  spełniona jest nierówność
spełniona jest nierówność
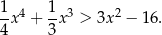
W kulę o promieniu długości 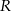 wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.
wpisano stożek o maksymalnej objętości. Oblicz objętość tego stożka.

