/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 28 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Parametr 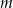 dobrano tak, że żadna liczba rzeczywista nie spełnia równania
dobrano tak, że żadna liczba rzeczywista nie spełnia równania
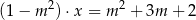
z niewiadomą  . Wynika stąd, że
. Wynika stąd, że
A) 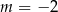 B)
B) 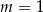 C)
C) 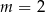 D)
D) 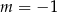
Reszta z dzielenia wielomianu 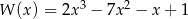 przez dwumian
przez dwumian 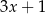 jest równa
jest równa
A) 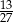 B)
B) 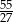 C)
C) 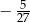 D)
D) 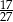
Wskaż rysunek, na którym przedstawiono fragment wykresu funkcji
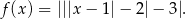
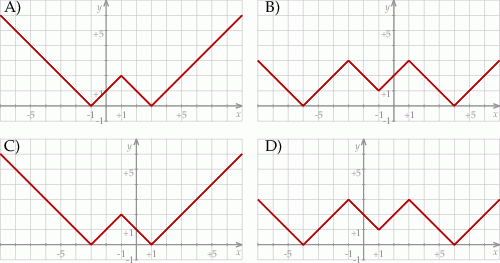
Wskaż liczbę, która spełnia równanie 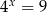 .
.
A) 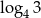 B)
B) 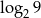 C)
C) 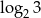 D)
D) 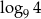
Wykres której z poniższych funkcji nie posiada asymptoty poziomej?
A) 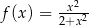 B)
B) 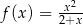 C)
C) 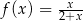 D)
D) 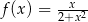
Zadania otwarte
Wśród uczniów pewnej szkoły przeprowadzono ankietę dotyczącą posiadanego rodzeństwa i okazało się, że:
– prawdopodobieństwo, że losowo wybrany uczeń ma brata jest równe 0,6;
– jeżeli wybierzemy losowo ucznia, który ma brata, to prawdopodobieństwo, że ten uczeń ma również siostrę jest równe 0,3;
– jeżeli wybierzemy losowo ucznia, który ma brata i ma siostrę, to prawdopodobieństwo, że ten uczeń jest uczniem klasy pierwszej jest równe 0,4.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany uczeń tej szkoły jest uczniem klasy pierwszej, który ma brata i siostrę.
Punkt 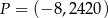 leży na paraboli o równaniu
leży na paraboli o równaniu 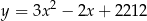 . Prosta o równaniu kierunkowym
. Prosta o równaniu kierunkowym 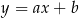 jest styczna do tej paraboli w punkcie
jest styczna do tej paraboli w punkcie 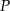 . Oblicz współczynnik
. Oblicz współczynnik 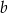 .
.
Iloczyn siedmiu kolejnych początkowych wyrazów pewnego ciągu geometrycznego wynosi 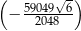 . Oblicz czwarty wyraz tego ciągu.
. Oblicz czwarty wyraz tego ciągu.
W urnie znajdują się 52 kule, które mogą się różnić wyłącznie kolorem. Wśród nich jest 26 kul białych, 6 kul czarnych, 12 niebieskich i 8 zielonych. Z tej urny losujemy czterokrotnie jedną kulę bez zwracania. Oblicz prawdopodobieństwo wylosowania czterech kul, wśród których są 2 białe i 2 niebieskie. Wynik podaj w postaci ułamka nieskracalnego.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 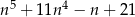 jest podzielne przez 16.
jest podzielne przez 16.
Niech 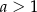 będzie ustaloną liczbą rzeczywistą i
będzie ustaloną liczbą rzeczywistą i 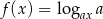 .
.
- Wyznacz dziedzinę funkcji
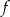 .
. - Oblicz
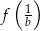 jeżeli
jeżeli 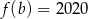 .
.
W  –kącie foremnym, gdzie
–kącie foremnym, gdzie 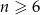 , iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz
, iloczyn liczby najdłuższych przekątnych przez liczbę najkrótszych przekątnych jest o 342 większy niż liczba osi symetrii tego wielokąta. Oblicz  .
.
Wykaż, że
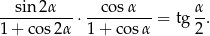
Wyznacz dziedzinę tej tożsamości.
W trapezie równoramiennym 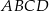 dłuższa podstawa
dłuższa podstawa 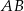 ma taką samą długość jak jego przekątna
ma taką samą długość jak jego przekątna 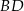 , a długość krótszej podstawy
, a długość krótszej podstawy 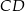 jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
jest równa wysokości trapezu. Oblicz w jakim stosunku dzielą się przekątne tego trapezu.
Długości boków trójkąta 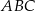 są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę
są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 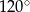 . Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta
. Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta 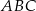 jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
Okrąg o równaniu 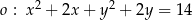 jest styczny do prostych
jest styczny do prostych 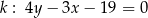 i
i 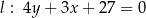 w punktach
w punktach 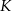 i
i 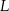 odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu
odpowiednio. Wyznacz równania wszystkich okręgów, które są jednocześnie styczne do okręgu  , prostych
, prostych 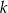 i
i 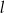 , oraz nie przechodzą przez punkty
, oraz nie przechodzą przez punkty 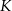 i
i 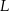 .
.
Rozważmy wszystkie graniastosłupy prawidłowe czworokątne o objętości 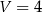 . Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.
. Wyznacz długości krawędzi tego z rozważanych graniastosłupów, którego pole powierzchni całkowitej jest najmniejsze. Oblicz to najmniejsze pole.

