/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 6 marca 2020 Czas pracy: 180 minut
Zadania zamknięte
Dane jest równanie 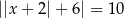 . Iloczyn rozwiązań tego równania jest równy
. Iloczyn rozwiązań tego równania jest równy
A) 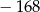 B)
B) 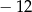 C) 216 D) 3024
C) 216 D) 3024
Jeśli 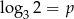 i
i 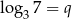 , to
, to 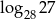 jest równy
jest równy
A) 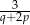 B)
B) 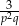 C)
C) 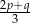 D)
D) 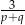
Suma kwadratów odwrotności pierwiastków równania 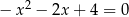 jest równa
jest równa
A) 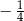 B)
B) 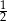 C)
C) 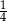 D)
D) 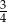
Dany jest trójkąt 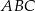 , w którym
, w którym 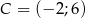 ,
, ![− → CB = [4 ;− 2 ]](https://img.zadania.info/zes/0062753/HzesT17x.gif) oraz środek ciężkości
oraz środek ciężkości 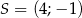 . Współrzędne wierzchołka
. Współrzędne wierzchołka  są równe
są równe
A) 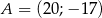 B)
B) 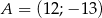 C)
C) 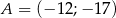 D)
D) 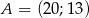
Zadania otwarte
Ze zbioru liczb: 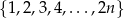 , gdzie
, gdzie 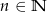 i
i 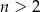 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 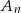 oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a
oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a 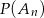 prawdopodobieństwo zajścia zdarzenia
prawdopodobieństwo zajścia zdarzenia 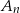 . Oblicz:
. Oblicz: 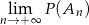 .
.
Przy dzieleniu wielomianu 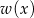 przez dwumian
przez dwumian 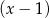 otrzymujemy resztę
otrzymujemy resztę 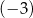 , przy dzieleniu przez dwumian
, przy dzieleniu przez dwumian 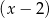 resztę 6, a przy dzieleniu przez dwumian
resztę 6, a przy dzieleniu przez dwumian 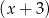 resztę 1. Wyznacz resztę z dzielenia wielomianu
resztę 1. Wyznacz resztę z dzielenia wielomianu 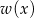 przez wielomian
przez wielomian 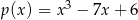 .
.
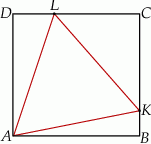
W prostokąt 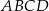 wpisany jest trójkąt równoboczny
wpisany jest trójkąt równoboczny 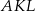 (patrz rysunek). Wierzchołek
(patrz rysunek). Wierzchołek 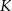 leży na boku
leży na boku 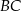 (
(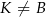 i
i 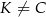 ), wierzchołek
), wierzchołek 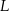 leży na boku
leży na boku 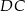 (
(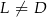 i
i 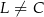 ). Udowodnij, że pole powierzchni trójkąta
). Udowodnij, że pole powierzchni trójkąta 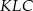 równe jest sumie pól trójkątów
równe jest sumie pól trójkątów 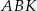 i
i 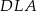 .
.
Rozwiąż równanie 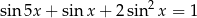 dla
dla 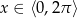 .
.
Dla jakiej wartości parametru 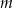 dwa różne pierwiastki
dwa różne pierwiastki 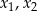 równania
równania
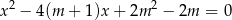
spełniają warunek 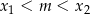 .
.
Przekątna 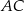 czworokąta
czworokąta 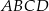 tworzy z bokiem
tworzy z bokiem 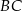 kąt
kąt 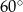 , a z bokiem
, a z bokiem 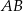 kąt
kąt 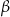 taki, że
taki, że 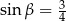 . Promień okręgu opisanego na trójkącie
. Promień okręgu opisanego na trójkącie 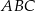 ma długość 5, a bok
ma długość 5, a bok 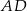 długość
długość 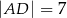 . Wiedząc, że w czworokąt
. Wiedząc, że w czworokąt 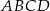 można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej
można wpisać okrąg oblicz długości pozostałych boków czworokąta oraz długość przekątnej 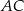 .
.
O funkcji 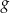 wiadomo, że
wiadomo, że 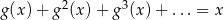 , gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru
, gdzie lewa strona równania jest sumą szeregu geometrycznego zbieżnego. Dla jakich wartości parametru 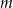 równanie
równanie 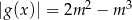 posiada dwa rozwiązania?
posiada dwa rozwiązania?
Styczne do okręgu o równaniu 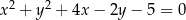 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 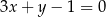 , przecinają prostą
, przecinają prostą 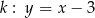 w punktach
w punktach 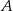 i
i 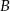 . Oblicz pole trójkąta
. Oblicz pole trójkąta 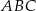 , jeśli
, jeśli 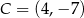 .
.
Ostrosłup prawidłowy czworokątny przecięto płaszczyzna przechodzącą przez krawędź podstawy i przecinającą przeciwległe krawędzie boczne w punktach jednakowo odległych od wierzchołka ostrosłupa. Przekrój ten jest trapezem o podstawach długości 12 i 8. Oblicz pole tego przekroju, jeżeli wysokość ostrosłupa ma długość 18.
Wiedząc, że 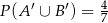 oraz
oraz 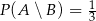 . Wykaż, że
. Wykaż, że 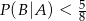 .
.
Na kole o promieniu 12 opisano trójkąt prostokątny. Oblicz długości boków tego trójkąta, którego pole jest najmniejsze.

