/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 23 kwietnia 2022 Czas pracy: 180 minut
Zadania zamknięte
Liczba 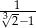 jest równa
jest równa
A) 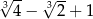 B)
B) 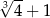 C)
C) 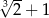 D)
D) 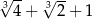
Na rysunku przedstawiono fragment wykresu funkcji 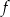 określonej dla każdej liczby rzeczywistej
określonej dla każdej liczby rzeczywistej  .
.
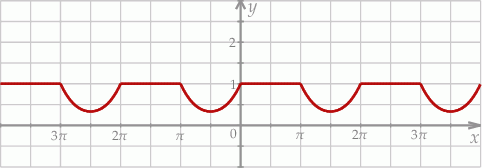
Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 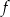 .
.
A) 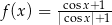 B)
B) 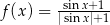 C)
C) 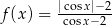 D)
D) 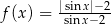
Granice 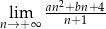 i
i 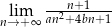 są równe. Stąd wynika, że
są równe. Stąd wynika, że
A) 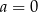 i
i 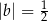 B)
B) 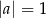 i
i 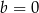 C)
C) 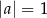 i
i 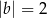 D)
D) 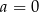 i
i 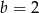
W turnieju szachowym rozegrano 45 partii. Każdy zawodnik rozegrał z każdym dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7
Zadania otwarte
Rozwiąż nierówność
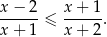
Wykaż, że jeżeli 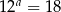 , to
, to 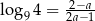 .
.
Dla jakich wartości parametru 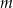 prosta
prosta 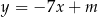 jest styczna do wykresu funkcji
jest styczna do wykresu funkcji 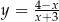 ?
?
Wyznacz wszystkie liczby rzeczywiste 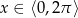 , które spełniają równanie
, które spełniają równanie
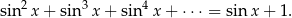
Łukasz w sposób losowy ustawia na jednej półce regału pewną liczbę książek. Wśród tych książek są trzy książki w języku angielskim, a wszystkie pozostałe są w języku polskim. Prawdopodobieństwo zdarzenia polegającego na tym, że trzy książki w języku angielskim znajdą się obok siebie jest równe 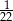 . Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
. Oblicz, ile książek w języku polskim zostało ustawionych na tej półce.
Prosta przechodząca przez punkty 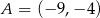 i
i 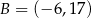 jest styczna do okręgu o środku w punkcie
jest styczna do okręgu o środku w punkcie 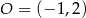 . Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą
. Oblicz promień tego okręgu i współrzędne punktu styczności tego okręgu z prostą 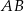 .
.
Podstawą graniastosłupa prawidłowego jest trójkąt, w którym wysokość ma długość 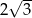 . Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt
. Przekątne ścian bocznych wychodzące z jednego wierzchołka tworzą kąt  taki, że
taki, że 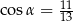 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
W deltoidzie 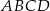 dane są
dane są 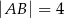 ,
, 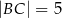 oraz
oraz 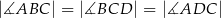 . Oblicz długość przekątnej
. Oblicz długość przekątnej 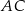 tego deltoidu.
tego deltoidu.
Czterowyrazowy ciąg 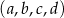 jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg
jest rosnący i arytmetyczny. Kwadrat największego wyrazu tego ciągu jest równy podwojonej sumie kwadratów pozostałych wyrazów tego ciągu. Ponadto ciąg 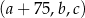 jest geometryczny. Oblicz wyrazy ciągu
jest geometryczny. Oblicz wyrazy ciągu 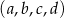 .
.
Dane są parabola o równaniu 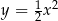 oraz punkty
oraz punkty 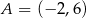 i
i 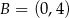 (zobacz rysunek).
(zobacz rysunek).
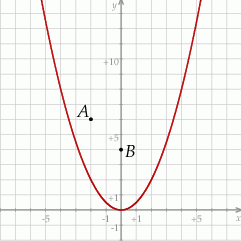
Rozpatrujemy wszystkie trójkąty 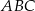 , których wierzchołek
, których wierzchołek 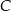 leży na tej paraboli. Niech
leży na tej paraboli. Niech 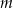 oznacza pierwszą współrzędną punktu
oznacza pierwszą współrzędną punktu 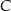 .
.
- Wyznacz pole
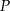 trójkąta
trójkąta 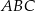 jako funkcję zmiennej
jako funkcję zmiennej 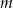 .
. - Wyznacz wszystkie wartości
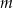 , dla których trójkąt
, dla których trójkąt 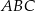 jest ostrokątny.
jest ostrokątny.
Rozpatrujemy wszystkie prostokąty 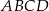 , których wierzchołki
, których wierzchołki 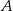 i
i 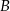 leżą na wykresie funkcji
leżą na wykresie funkcji 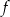 określonej wzorem
określonej wzorem 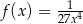 dla
dla 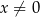 . Punkty
. Punkty 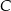 i
i 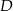 leżą na wykresie funkcji
leżą na wykresie funkcji 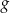 określonej wzorem
określonej wzorem 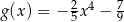 i są położone symetrycznie względem osi
i są położone symetrycznie względem osi 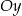 (zobacz rysunek). Oblicz współrzędne wierzchołka
(zobacz rysunek). Oblicz współrzędne wierzchołka 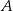 , dla którego pole prostokąta
, dla którego pole prostokąta 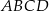 jest najmniejsze. Oblicz to najmniejsze pole.
jest najmniejsze. Oblicz to najmniejsze pole.