/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 27 kwietnia 2024 Czas pracy: 180 minut
Oblicz granicę 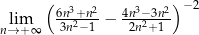 .
.
Wielomian 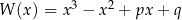 można dwukrotnie podzielić bez reszty przez dwumian
można dwukrotnie podzielić bez reszty przez dwumian 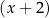 . Oblicz
. Oblicz 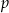 i
i 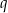 .
.
Czworokąt 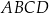 jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach
jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach 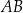 i
i 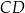 są styczne zewnętrznie, to równoległobok
są styczne zewnętrznie, to równoległobok 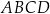 jest rombem.
jest rombem.
Liczby rzeczywiste  oraz
oraz 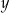 spełniają jednocześnie równanie
spełniają jednocześnie równanie 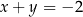 i nierówność
i nierówność
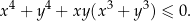
Wykaż, że 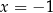 oraz
oraz 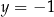 .
.
Prawdopodobieństwo wystąpienia awarii oświetlenia ulic w pewnym mieście w godzinach wieczornych pojedynczego dnia jest równe 0,2. Oblicz prawdopodobieństwo zdarzenia 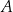 polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
polegającego na tym, że w okresie sześciu dni wystąpią co najwyżej trzy takie dni, w których nastąpi awaria oświetlenia ulic w tym mieście w godzinach wieczornych. Wynik podaj w ułamku dziesiętnym w zaokrągleniu do części setnych.
Rozwiąż równanie 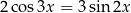 w przedziale
w przedziale ![[20 23π ,2 024π ]](https://img.zadania.info/zes/0064723/HzesT17x.png)
Dany jest nieskończony szereg geometryczny
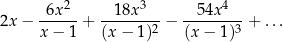
Wyznacz wszystkie wartości zmiennej  (różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest różna od 0,3.
(różnej od 0 i od 1), dla których suma tego szeregu istnieje i jest różna od 0,3.
Czworokąt 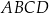 , w którym
, w którym 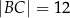 i
i 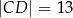 , jest opisany na okręgu. Przekątna
, jest opisany na okręgu. Przekątna 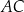 tego czworokąta tworzy z bokiem
tego czworokąta tworzy z bokiem 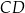 kąt, którego tangens jest równy
kąt, którego tangens jest równy 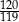 . Tangens kąta
. Tangens kąta 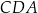 jest równy
jest równy 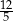 . Oblicz długość odcinka
. Oblicz długość odcinka 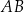 .
.
Ze zbioru liczb 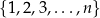 , dla
, dla 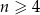 losujemy bez zwracania dwie liczby
losujemy bez zwracania dwie liczby  i
i 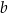 . Oblicz
. Oblicz  jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby
jeżeli wiadomo, że prawdopodobieństwo tego, że wylosowane liczby  i
i 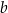 spełniają nierówność
spełniają nierówność
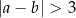
jest równe 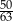 .
.
W graniastosłupie prawidłowym sześciokątnym 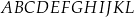 płaszczyzna
płaszczyzna 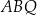 przechodzi przez krawędź
przechodzi przez krawędź 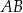 i przez środek
i przez środek 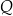 krawędzi
krawędzi 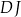 (zobacz rysunek).
(zobacz rysunek).
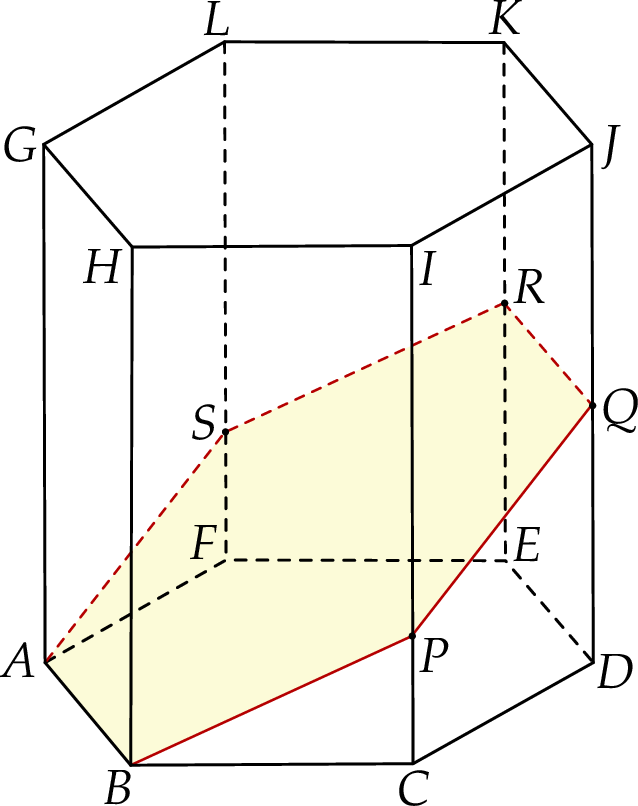
Stosunek pola przekroju graniastosłupa płaszczyzną 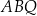 do pola jego podstawy jest równy
do pola jego podstawy jest równy 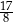 . Oblicz objętość graniastosłupa
. Oblicz objętość graniastosłupa 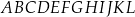 , jeżeli jego krawędź boczna ma długość
, jeżeli jego krawędź boczna ma długość 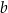 .
.
Funkcja 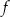 jest określona wzorem
jest określona wzorem
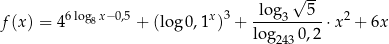
dla każdej liczby ![[ ] x ∈ 12,3](https://img.zadania.info/zes/0064723/HzesT50x.png) . Wyznacz zbiór wartości funkcji
. Wyznacz zbiór wartości funkcji 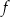 .
.
Wyznacz wszystkie wartości parametru 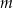 , dla których równanie
, dla których równanie
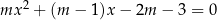
ma dokładnie dwa różne rozwiązania rzeczywiste 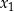 oraz
oraz 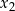 , spełniające warunki:
, spełniające warunki:
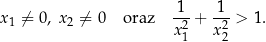
Rozważamy wszystkie proste na płaszczyźnie, które są jednocześnie styczne do wykresu funkcji homograficznej 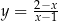 oraz do okręgu o równaniu
oraz do okręgu o równaniu 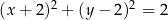 . Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.
. Wyznacz równania tych spośród rozważanych prostych, których współczynniki kierunkowe są liczbami wymiernymi.

