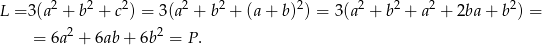/Szkoła średnia

Zadanie nr 7613150

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że jeśli 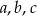a,b,c są dowolnymi liczbami rzeczywistymi takimi, że 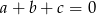a + b + c = 0 , to

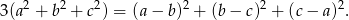
3(a2 + b2 + c2) = (a − b)2 + (b− c)2 + (c − a)2.

Rozwiązanie

Sposób I

Przekształcamy równość, którą mamy udowodnić w sposób równoważny.

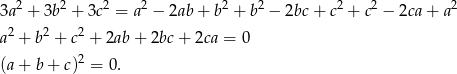
2 2 2 2 2 2 2 2 2 3a + 3b + 3c = a − 2ab + b + b − 2bc+ c + c − 2ca + a a2 + b2 + c2 + 2ab + 2bc + 2ca = 0 2 (a+ b+ c) = 0.

Na koniec skorzystaliśmy ze wzoru na kwadrat sumy. Otrzymana równość jest oczywiście spełniona, a przekształcaliśmy ją w sposób równoważny, więc wyjściowa równość też musi być spełniona.

Sposób II

Przekształcamy prawą stronę równości, którą mamy udowodnić podstawiając 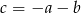c = −a − b .

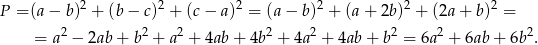
2 2 2 2 2 2 P = (a − b) + (b − c) + (c− a) = (a− b ) + (a + 2b) + (2a + b) = = a 2 − 2ab + b 2 + a2 + 4ab + 4b 2 + 4a 2 + 4ab + b2 = 6a2 + 6ab + 6b2.

Teraz wykonujemy takie same podstawienie w lewej stronie równości

L = 3(a2 + b2 + c2) = 3(a2 + b2 + (a+ b )2) = 3(a2 + b2 + a 2 + 2ba + b2) = 2 2 = 6a + 6ab + 6b = P .
Wersja PDF