/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 5 marca 2016 Czas pracy: 180 minut
Zadania zamknięte
Granica 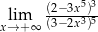 jest równa
jest równa
A) 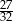 B)
B)  C)
C) 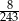 D)
D) 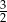
Liczba punktów wspólnych wykresów funkcji 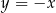 i
i 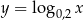 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Liczba 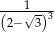 jest równa
jest równa
A) 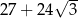 B)
B) 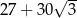 C)
C) 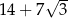 D)
D) 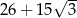
Pochodna funkcji 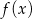 jest równa
jest równa 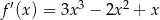 . Funkcja
. Funkcja 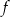 może mieć wzór
może mieć wzór
A) 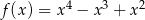 B)
B) 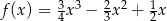
C) 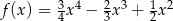 D)
D) 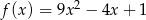
Liczba 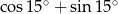 jest równa
jest równa
A) 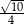 B)
B) 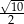 C)
C) 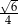 D)
D) 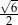
Zadania otwarte
Prosta o równaniu 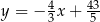 jest styczna od okręgu o środku
jest styczna od okręgu o środku 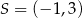 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Wyznacz najmniejszą liczbę całkowitą  spełniającą równanie
spełniającą równanie
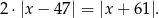
W każdej z dwóch urn jest tyle samo kul białych i czarnych, a trzecia urna jest pusta. Z każdej z dwóch pierwszych urn losujemy jedną kulę i wkładamy je do trzeciej urny. Następnie z trzeciej urny losujemy jedną kulę. Oblicz prawdopodobieństwo tego, że kula wylosowana z trzeciej urny jest biała.
Oblicz granicę 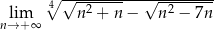 .
.
Wykaż, że jeżeli 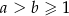 , to
, to 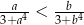 .
.
Niech 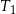 będzie trójkątem równobocznym o boku długości
będzie trójkątem równobocznym o boku długości  . Konstruujemy kolejno trójkąty równoboczne
. Konstruujemy kolejno trójkąty równoboczne 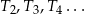 takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów
takie, że bok kolejnego trójkąta jest równy wysokości poprzedniego trójkąta. Oblicz sumę pól wszystkich tak utworzonych trójkątów 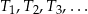 .
.
Długości boków czworokąta 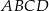 są równe:
są równe: 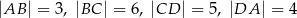 . Na czworokącie
. Na czworokącie 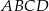 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 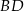 tego czworokąta.
tego czworokąta.
Wyznacz wszystkie wartości parametru 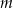 , dla których równanie
, dla których równanie 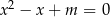 ma dwa rozwiązania rzeczywiste
ma dwa rozwiązania rzeczywiste 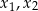 spełniające warunek
spełniające warunek 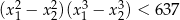 .
.
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych nieparzystych, w których zapisie występują co najmniej trzy jedynki.
Punkty 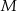 i
i 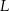 leżą odpowiednio na bokach
leżą odpowiednio na bokach 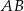 i
i 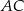 trójkąta
trójkąta 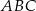 , przy czym zachodzą równości
, przy czym zachodzą równości 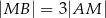 oraz
oraz 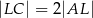 . Punkt
. Punkt 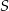 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 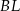 i
i 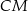 . Punkt
. Punkt 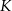 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 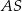 z odcinkiem
z odcinkiem  (zobacz rysunek).
(zobacz rysunek).
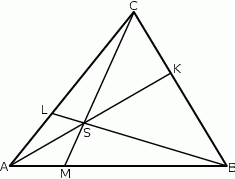
Pole trójkąta 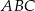 jest równe 528. Oblicz pola trójkątów:
jest równe 528. Oblicz pola trójkątów: 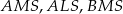 i
i 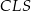 .
.
Podstawą ostrosłupa 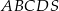 jest trapez równoramienny
jest trapez równoramienny 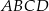 , którego ramiona mają długość
, którego ramiona mają długość 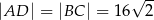 i tworzą z podstawą
i tworzą z podstawą 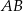 kąt ostry o mierze
kąt ostry o mierze 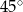 . Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem
. Każda ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod tym samym kątem  takim, że
takim, że 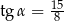 . Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego ściany bocznej 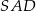 .
.
Dany jest prostokątny arkusz kartonu o długości 64 cm i szerokości 40 cm. Po dwóch stronach tego arkusza wycięto prostokąty, w których stosunek boków jest równy 1:2 (zacieniowane prostokąty na rysunku).

Następnie zagięto karton wzdłuż linii przerywanych, tworząc w ten sposób prostopadłościenne pudełko (bez przykrywki). Oblicz długości boków wyciętych prostokątów, dla których objętość otrzymanego pudełka jest największa. Oblicz tę objętość.

