Zadanie nr 9286767
Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.
Rozwiązanie
Przyjmijmy, że zdarzenia elementarne to uporządkowane pary wylosowanych liczb. Zatem
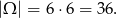
Jeżeli iloczyn wyrzuconych liczb oczek ma być nieparzysty to oba wyniki muszą liczbami nieparzystymi. Ponadto co najmniej jedna z tych liczb musi być równa 5, bo inaczej maksymalnie mielibyśmy 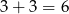 . Mamy zatem 3 zdarzenia sprzyjające
. Mamy zatem 3 zdarzenia sprzyjające
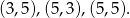
Zatem prawdopodobieństwo wynosi
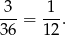
Odpowiedź: