Zadanie nr 9615938
Dany jest nieskończony rosnący ciąg arytmetyczny 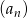 , dla
, dla 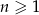 taki, że
taki, że 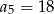 . Wyrazy
. Wyrazy 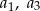 oraz
oraz 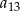 tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na
tego ciągu są odpowiednio pierwszym, drugim i trzecim wyrazem pewnego ciągu geometrycznego. Wyznacz wzór na  –ty wyraz ciągu
–ty wyraz ciągu 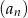 .
.
Rozwiązanie
Wiemy, że 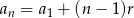 dla pewnej liczby
dla pewnej liczby 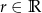 . Wiemy też, że liczby
. Wiemy też, że liczby 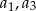 i
i 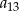 są kolejnymi wyrazami ciągu geometrycznego, więc
są kolejnymi wyrazami ciągu geometrycznego, więc
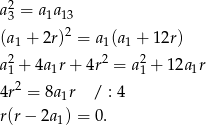
Ponieważ z założenia ciąg 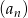 jest rosnący, mamy stąd
jest rosnący, mamy stąd 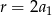 . Pozostało skorzystać z warunku
. Pozostało skorzystać z warunku 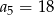 . Mamy zatem
. Mamy zatem
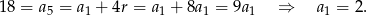
Stąd 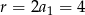 i
i 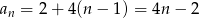 .
.
Odpowiedź: 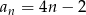 dla
dla