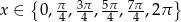Zadanie nr 9789961
Rozwiąż równanie 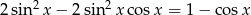 w przedziale
w przedziale 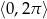 .
.
Rozwiązanie
Sposób I
Korzystając z jedynki trygonometrycznej możemy dane równanie zapisać w postaci
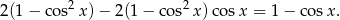
Podstawmy teraz 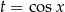
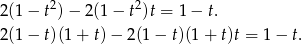
Widać, że każdy składnik jest podzielny przez 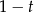 , zatem
, zatem 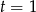 jest jednym z rozwiązań równania.
jest jednym z rozwiązań równania.
Jeżeli teraz założymy, że 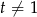 to możemy podzielić równanie stronami przez
to możemy podzielić równanie stronami przez 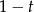 . Otrzymamy wtedy
. Otrzymamy wtedy
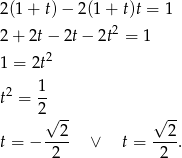
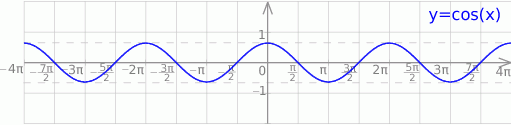
Szkicujemy teraz funkcję cosinus i odczytujemy z wykresu rozwiązania równań 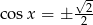 i
i 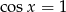 w podanym przedziale
w podanym przedziale 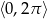 .
.
Rozwiązaniami równania są
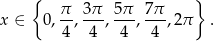
Sposób II
Tym razem przekształcimy równanie nie podstawiając za cosinus.
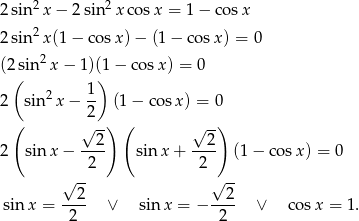
Rozwiązania tych równań znajdujemy tak samo jak w I sposobie.
Odpowiedź: