/Szkoła średnia
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 27 kwietnia 2024 Czas pracy: 180 minut
Wśród podanych poniżej nierówności wskaż tę, której zbiorem rozwiązań jest przedział 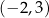 .
.
A) 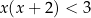 B)
B) 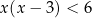 C)
C) 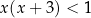 D)
D) 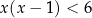
Liczba 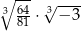 jest równa
jest równa
A) 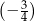 B)
B)  C)
C)  D)
D) 
Liczba 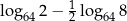 jest równa
jest równa
A) 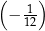 B)
B) 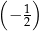 C)
C) 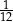 D)
D) 
Wskaż nierówność, która opisuje sumę przedziałów zaznaczonych na osi liczbowej.

A) 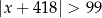 B)
B) 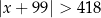 C)
C) 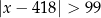 D)
D) 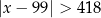
Informacja do zadań 5.1 i 5.2
W kartezjańskim układzie współrzędnych  narysowano wykres funkcji
narysowano wykres funkcji 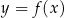 (zobacz rysunek).
(zobacz rysunek).
Wyznacz zbiór rozwiązań nierówności  .
.
Funkcja  jest malejąca w zbiorze
jest malejąca w zbiorze
A) ![[5,6]](https://img.zadania.info/zes/0098070/HzesT25x.png) B)
B) ![[−1 ,7]](https://img.zadania.info/zes/0098070/HzesT26x.png) C)
C) ![[4,7]](https://img.zadania.info/zes/0098070/HzesT27x.png) D)
D) ![[− 3,4]](https://img.zadania.info/zes/0098070/HzesT28x.png)
Wyrażenie 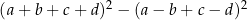 może być zapisane w postaci
może być zapisane w postaci
A) 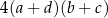 B)
B) 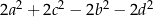
C) 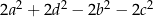 D)
D) 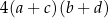
Wykaż, że dla każdej liczby całkowitej 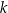 reszta z dzielenia liczby
reszta z dzielenia liczby 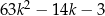 przez 7 jest równa 4.
przez 7 jest równa 4.
Dany jest wielomian 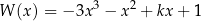 , gdzie
, gdzie 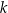 jest pewną liczbą rzeczywistą. Wiadomo, że wielomian
jest pewną liczbą rzeczywistą. Wiadomo, że wielomian 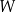 można zapisać w postaci
można zapisać w postaci 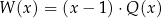 dla pewnego wielomianu
dla pewnego wielomianu 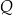 . Liczba
. Liczba 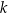 jest równa
jest równa
A) 29 B) 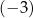 C) 0 D) 3
C) 0 D) 3
Wykresem funkcji kwadratowej 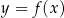 jest parabola o wierzchołku w punkcie
jest parabola o wierzchołku w punkcie 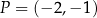 . Prosta
. Prosta 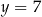 przecina tę parabolę w punktach
przecina tę parabolę w punktach 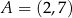 i
i 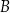 . Długość odcinka
. Długość odcinka 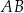 jest równa
jest równa
A) 18 B) 6 C) 10 D) 8
Dwa boki trójkąta 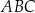 są zawarte w prostych
są zawarte w prostych 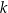 i
i 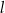 o równaniach
o równaniach
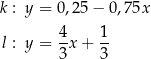
Dokończ zdanie. Wybierz odpowiedź A albo B oraz odpowiedź 1., 2. albo 3.
Trójkąt 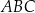
| A) jest prostokątny | B) nie jest prostokątny |
i jeden z jego wierzchołków może mieć współrzędne
1. 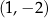 | 2. 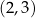 | 3. 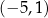 |
Na rysunku przedstawiono geometryczną interpretację jednego z niżej zapisanych układów równań.
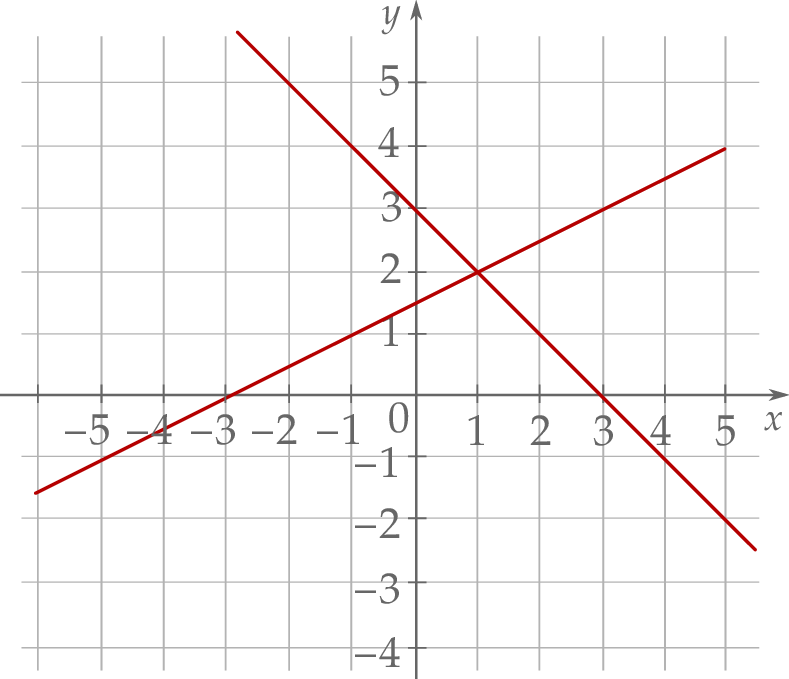
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A) 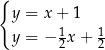 B)
B) 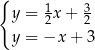 C)
C) 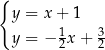 D)
D) 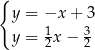
Równanie 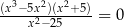 w zbiorze liczb rzeczywistych ma dokładnie
w zbiorze liczb rzeczywistych ma dokładnie
A) jedno rozwiązanie.
B) dwa rozwiązania.
C) trzy rozwiązania.
D) cztery rozwiązania.
Dla każdej liczby rzeczywistej  różnej od
różnej od 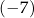 i 7 wartość wyrażenia
i 7 wartość wyrażenia
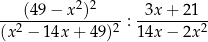
jest równa wartości wyrażenia
A) 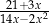 B)
B) 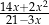 C)
C) 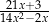 D)
D) 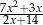
Ciąg 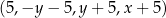 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Proces stygnięcia naparu z ziół w otoczeniu o stałej temperaturze 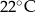 opisuje funkcja wykładnicza
opisuje funkcja wykładnicza 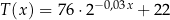 , gdzie
, gdzie 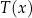 to temperatura naparu wyrażona w stopniach Celsjusza po
to temperatura naparu wyrażona w stopniach Celsjusza po  minutach liczonych od momentu
minutach liczonych od momentu 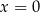 , w którym zioła zalano wrzątkiem. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
, w którym zioła zalano wrzątkiem. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Temperatura naparu po 35 minutach od momentu zalania ziół wrzątkiem jest większa od 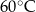 . . | P | F |
Temperatura naparu po 2 godzinach od momentu zalania ziół wrzątkiem jest mniejsza od 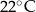 . . | P | F |
Funkcje 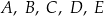 oraz
oraz 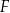 są określone dla każdej liczby rzeczywistej
są określone dla każdej liczby rzeczywistej  . Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
. Wzory tych funkcji podano poniżej. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Przedział 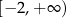 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
A) 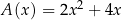 B)
B) 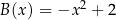 C)
C) 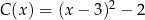
D) 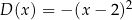 E)
E) 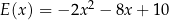 F)
F) 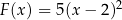
W kartezjańskim układzie współrzędnych 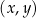 zaznaczono kąt
zaznaczono kąt  o wierzchołku w punkcie
o wierzchołku w punkcie 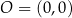 . Jedno z ramion tego kąta pokrywa się z dodatnią półosią
. Jedno z ramion tego kąta pokrywa się z dodatnią półosią 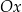 , a drugie przechodzi przez punkt
, a drugie przechodzi przez punkt 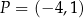 (zobacz rysunek).
(zobacz rysunek).
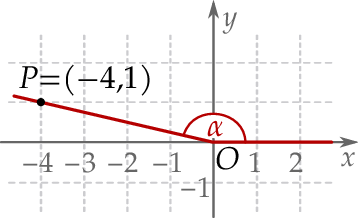
Tangens kąta  jest równy
jest równy
A) 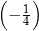 B)
B) 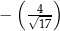 C)
C) 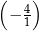 D)
D) 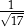
Informacja do zadań 18.1 i 18.2
Na rysunkach A–F w kartezjańskim układzie współrzędnych 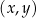 zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią
zaznaczono różne kąty. Jedno z ramion każdego z tych kątów pokrywa się z dodatnią półosią 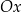 , a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych:
, a drugie przechodzi przez jeden z punktów o współrzędnych całkowitych: 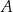 lub
lub 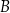 , lub
, lub 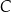 , lub
, lub 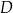 , lub
, lub 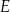 , lub
, lub 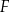 .
.
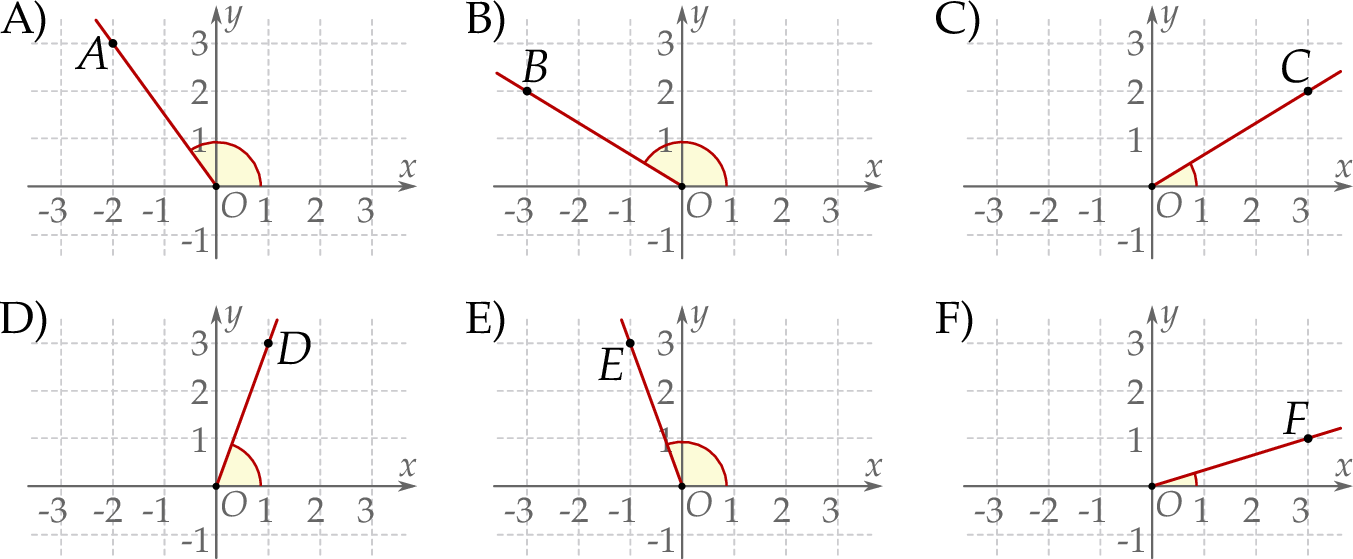
Na którym rysunku zaznaczono kąt  , spełniający warunek
, spełniający warunek 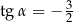 ?
?
Na którym rysunku zaznaczono kąt 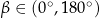 , spełniający warunek
, spełniający warunek 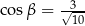 ?
?
Wszystkich różnych liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym przynajmniej jedna cyfra występuje dwa razy jest
A) 252 B) 180 C) 171 D) 396
Arkusz blachy ma kształt trójkąta prostokątnego 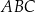 , w którym
, w którym 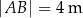 i
i 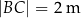 . Z tego arkusza należy wyciąć trójkąt równoramienny
. Z tego arkusza należy wyciąć trójkąt równoramienny 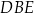 w ten sposób, że punkty
w ten sposób, że punkty 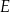 i
i 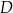 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 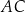 i
i 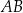 oraz
oraz 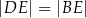 (zobacz rysunek).
(zobacz rysunek).
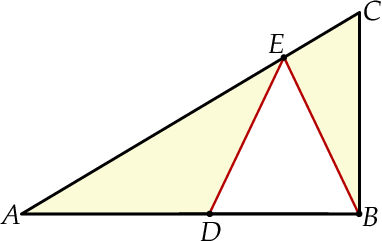
Oblicz jaką długość powinna mieć podstawa 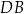 trójkąta
trójkąta 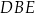 tak, aby jego pole było największe możliwe. Oblicz to największe pole.
tak, aby jego pole było największe możliwe. Oblicz to największe pole.
Wszystkie wierzchołki kwadratu 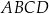 mają współrzędne nieujemne, przy czym
mają współrzędne nieujemne, przy czym 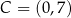 i
i 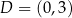 . Okrąg wpisany w kwadrat
. Okrąg wpisany w kwadrat 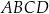 jest określony równaniem
jest określony równaniem
A) 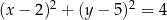 B)
B) 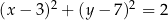
C) 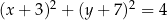 D)
D) 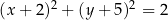
Ciąg 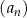 jest określony wzorem
jest określony wzorem 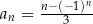 dla każdej liczby naturalnej
dla każdej liczby naturalnej 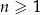 . Liczba wyrazów tego ciągu mniejszych od 12 jest równa
. Liczba wyrazów tego ciągu mniejszych od 12 jest równa
A) 36 B) 34 C) 33 D) 35
Rozwiąż równanie 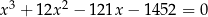 .
.
Pole równoległoboku  jest równe
jest równe 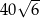 . Bok
. Bok 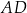 tego równoległoboku ma długość 10, a kąt
tego równoległoboku ma długość 10, a kąt 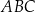 równoległoboku ma miarę
równoległoboku ma miarę 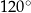 (zobacz rysunek).
(zobacz rysunek).

Długość boku 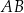 jest równa
jest równa
A) 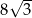 B)
B) 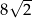 C)
C) 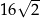 D)
D) 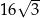
Ciąg geometryczny 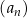 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 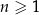 . W tym ciągu
. W tym ciągu 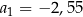 oraz
oraz 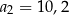 . Suma trzech początkowych wyrazów ciągu
. Suma trzech początkowych wyrazów ciągu 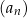 jest równa
jest równa
A) 48,45 B) 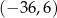 C) 7,65 D)
C) 7,65 D) 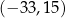
W okręgu  kąt środkowy
kąt środkowy 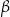 oraz kąt wpisany
oraz kąt wpisany  są oparte na tym samym łuku. Kąt
są oparte na tym samym łuku. Kąt 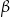 ma miarę o
ma miarę o 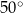 większą od kąta
większą od kąta  . Miara kąta
. Miara kąta 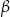 jest równa
jest równa
A) 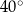 B)
B) 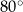 C)
C) 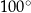 D)
D) 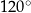
Doświadczenie losowe polega na czterokrotnym rzucie symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Prawdopodobieństwo zdarzenia polegającego na tym, że iloczyn liczb wyrzuconych oczek jest liczbą nieparzystą, jest równe
A) 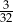 B)
B) 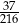 C)
C) 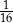 D)
D) 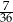
Wykresy funkcji 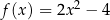 i
i 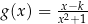 określonych dla każdej liczby rzeczywistej
określonych dla każdej liczby rzeczywistej  przecinają się w dwóch punktach – jednym z nich jest punkt
przecinają się w dwóch punktach – jednym z nich jest punkt 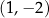 . Liczba
. Liczba 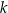 jest równa
jest równa
A) 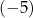 B) 5 C)
B) 5 C) 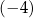 D) 4
D) 4
W trapezie 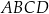 podstawa
podstawa 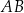 jest dłuższa od podstawy
jest dłuższa od podstawy 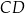 . Przekątne trapezu przecinają się w punkcie
. Przekątne trapezu przecinają się w punkcie 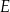 (zobacz rysunek).
(zobacz rysunek).
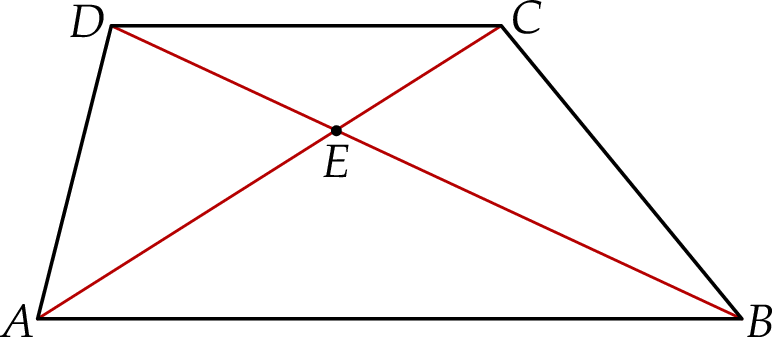
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 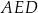 jest równe polu trójkąta jest równe polu trójkąta 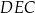 . . | P | F |
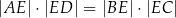 | P | F |
Dany jest graniastosłup prawidłowy sześciokątny 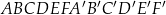 , w którym krawędź podstawy ma długość 5. Przekątna
, w którym krawędź podstawy ma długość 5. Przekątna 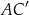 tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem
tego graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem 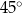 (zobacz rysunek).
(zobacz rysunek).

Objętość tego graniastosłupa jest równa
A) 225 B) 562,5 C) 112,5 D) 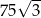
Dany jest okrąg 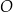 o środku w punkcie
o środku w punkcie 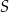 . Średnica
. Średnica 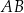 tego okręgu przecina cięciwę
tego okręgu przecina cięciwę 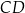 w punkcie
w punkcie 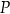 (zobacz rysunek). Ponadto:
(zobacz rysunek). Ponadto: 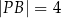 ,
, 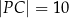 oraz
oraz 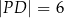 .
.
Oblicz promień okręgu 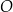 .
.
Średnia arytmetyczna liczb: 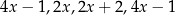 i
i 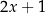 zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
zwiększa się o 1 jeżeli pominiemy ostatnią liczbę. Wynika stąd, że
A) 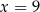 B)
B) 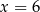 C)
C) 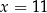 D)
D) 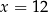
Punkty 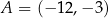 ,
, 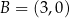 i
i 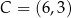 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 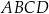 . Wierzchołek
. Wierzchołek 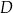 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 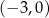 B)
B) 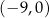 C)
C) 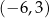 D)
D) 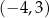
Ze zbioru liczb 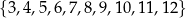 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 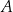 polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.
polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 3.

