/Szkoła średnia

Zadanie nr 9818515

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma długości dwóch boków trójkąta równa się 4, a kąt między tymi bokami ma miarę 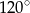1 20∘ . Oblicz najmniejszą wartość sumy kwadratów długości wszystkich boków tego trójkąta.

Rozwiązanie

Szkicujemy trójkąt.

PIC

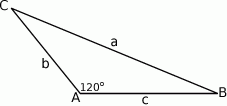
Przy oznaczeniach z rysunku, na mocy twierdzenia cosinusów mamy

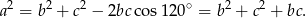
a2 = b2 + c2 − 2bcco s120∘ = b2 + c2 + bc.

W takim razie suma kwadratów długości boków trójkąta jest równa

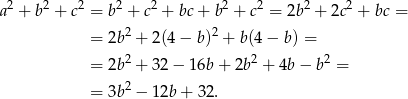
2 2 2 2 2 2 2 2 2 a + b + c = b + c + bc + b + c = 2b + 2c + bc = = 2b2 + 2(4 − b)2 + b(4− b) = = 2b2 + 32 − 16b + 2b2 + 4b − b2 = 2 = 3b − 12b + 32.

Dziedziną tej funkcji jest przedział 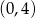(0 ,4) , a jej wykresem parabola o ramionach skierowanych do góry i wierzchołku w punkcie

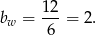
bw = 12-= 2. 6

Minimalna suma kwadratów długości boków jest wtedy równa

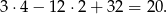
3⋅4 − 12 ⋅2 + 32 = 20.

 
Odpowiedź: 20

Wersja PDF