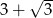/Szkoła średnia

Zadanie nr 9862046

Dodaj do ulubionych
Dodaj do rozwiązanych

Długość krawędzi sześcianu jest o 2 krótsza od długości jego przekątnej. Oblicz długość przekątnej tego sześcianu.

Rozwiązanie

Zaczynamy od rysunku

PIC

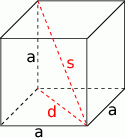
Długość przekątnej podstawy jest dana wzorem

√ -- d = a 2.

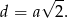
Zatem na mocy twierdzenia Pitagorasa, przekątna sześcianu jest dana wzorem

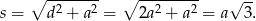
∘ -------- ∘ --------- √ -- s = d2 + a2 = 2a 2 + a 2 = a 3.

Korzystamy z założenia i otrzymujemy równanie

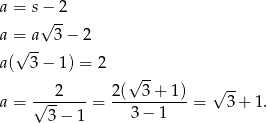
a = s− 2 √ -- a =√ a 3 − 2 a( 3− 1) = 2 √ -- ---2---- 2(--3-+-1)- √ -- a = √ 3 − 1 = 3− 1 = 3+ 1.

Przekątna sześcianu ma więc długość

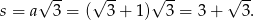
√ -- √ -- √ -- √ -- s = a 3 = ( 3 + 1) 3 = 3+ 3.

 
Odpowiedź: √ -- 3 + 3

Wersja PDF