/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 1 maja 2010 Czas pracy: 180 minut
- Narysuj wykresy funkcji
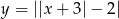 oraz
oraz 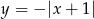 , gdzie
, gdzie 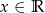 .
. - Wyznacz te wartości parametru
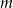 , dla których równanie
, dla których równanie 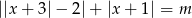 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Wyznacz środek okręgu wpisanego w trójkąt, którego boki zwierają się w prostych o równaniach 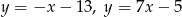 oraz
oraz 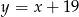 .
.
Dwa przeciwległe boki czworokąta wpisanego w okrąg mają równe długości. Wykaż, że czworokąt ten jest trapezem.
Korzystając ze wzoru
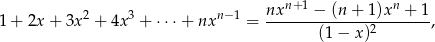
który jest prawdziwy dla dowolnej liczby naturalnej  i dowolnej liczby
i dowolnej liczby 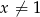 , wykaż, że
, wykaż, że
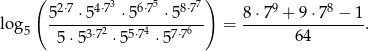
Kwadrat o wierzchołkach 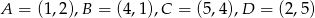 przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach
przekształcono w jednokładności o skali ujemnej i otrzymano kwadrat o wierzchołkach 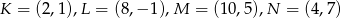 . Wyznacz środek i skalę tej jednokładności.
. Wyznacz środek i skalę tej jednokładności.
Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 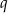 , a cosinus jednego z jego kątów jest równy
, a cosinus jednego z jego kątów jest równy 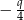 .
.
- Wyznacz
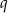 .
. - Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość
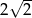 , oblicz pole tego trójkąta.
, oblicz pole tego trójkąta.
Wyznacz wszystkie wartości parametru 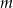 , dla których równanie
, dla których równanie
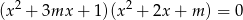
ma cztery różne pierwiastki, których suma sześcianów jest równa 4.
W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.
Rozwiąż nierówność 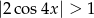 .
.
Umieszczamy króla szachowego w lewym dolnym rogu 64-polowej szachownicy, a następnie siedem razy przesuwamy go losowo w górę lub w prawo (za każdym razem na nowo losujemy kierunek przesunięcia).

Zakładając, że wylosowanie każdego kierunku jest jednakowo prawdopodobne, oblicz prawdopodobieństwo, że na końcu król nie znajdzie się w rogu szachownicy.

