/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna

Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 24 kwietnia 2010 Czas pracy: 180 minut

Zadanie 1
(5 pkt)

W prostokątnym układzie współrzędnych zaznacz zbiór wszystkich punktów, których współrzędne spełniają warunek 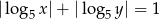|log5 x|+ |log 5y| = 1 .

PIC

Zadanie 2
(3 pkt)

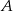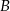Do dwóch okręgów przecinających się w punktach A i B poprowadzono wspólną styczną 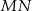MN , przy czym punkt 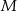M należy do pierwszego, a punkt 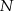N do drugiego okręgu. Wykaż, że prosta 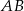AB dzieli odcinek 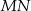MN na połowy.

Zadanie 3
(6 pkt)

Wyznacz największą wartość funkcji

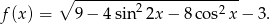
∘ ----------------------- f(x) = 9− 4sin22x − 8cos2 x− 3.

Zadanie 4
(4 pkt)

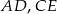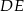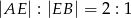Trójkąt podzielono odcinkami AD ,CE i DE na 5 trójkątów, przy czym |AE | : |EB | = 2 : 1 .

PIC

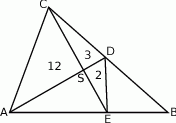
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 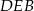DEB .

Zadanie 5
(4 pkt)

Malarz chcąc rozjaśnić 20 litrów granatowej farby postąpił w następujący sposób: odlał jeden litr farby i dolał 1 litr farby białej, a potem całość dokładnie wymieszał. Procedurę tę powtórzył w sumie 8 razy. Ile litrów granatowej farby pozostało w otrzymanej mieszaninie? Wynik podaj z dokładnością do 1 litra.

Zadanie 6
(5 pkt)

W sferę o promieniu 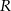R wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość √ -- 5 3 , oblicz R .

Zadanie 7
(4 pkt)

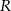Wykaż, że równanie 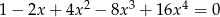1 − 2x + 4x 2 − 8x3 + 16x4 = 0 nie ma rozwiązań rzeczywistych.

Zadanie 8
(6 pkt)

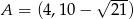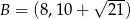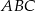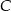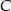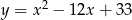Punkty √ --- A = (4,10− 21) i B = (8,10 + √ 21) są wierzchołkami trójkąta prostokątnego ABC , o kącie prostym przy wierzchołku C . Oblicz współrzędne wierzchołka C tego trójkąta, wiedząc, że leży on na paraboli o równaniu 2 y = x − 12x + 3 3 .

Zadanie 9
(5 pkt)

Spośród wyrazów skończonego ciągu arytmetycznego 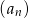(an) danego wzorem 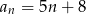an = 5n + 8 , gdzie 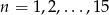n = 1,2,...,15 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.

Zadanie 10
(3 pkt)

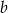Wykaż, że jeżeli liczby a i b spełniają równość 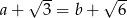√ -- √ -- a + 3 = b+ 6 to przynajmniej jedna z nich jest niewymierna.

Zadanie 11
(5 pkt)

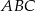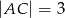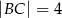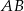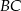W trójkąt prostokątny ABC o przyprostokątnych długości |AC | = 3 i |BC | = 4 wpisano dwa przystające okręgi w ten sposób, że są one wzajemnie styczne oraz jeden z nich jest styczny do boków AB i BC , a drugi do boków 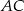AC i BC .

PIC

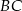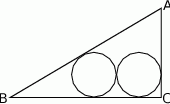
Oblicz długość promienia tych okręgów.

Arkusz Wersja PDF
Rozwiązania