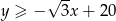Zadanie nr 7094091
Dane są punkty 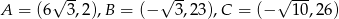 . Opisz za pomocą nierówności półpłaszczyznę o krawędzi
. Opisz za pomocą nierówności półpłaszczyznę o krawędzi 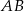 , do której należy punkt
, do której należy punkt 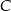 .
.
Rozwiązanie
Ze względu na duże liczby i pierwiastki trudno o dokładny rysunek, więc rozpocznijmy od napisania równania prostej 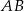 . Można to zrobić korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale my obejdziemy się bez niego. Szukamy prostej w postaci
. Można to zrobić korzystając ze wzoru na równanie prostej przechodzącej przez dwa punkty, ale my obejdziemy się bez niego. Szukamy prostej w postaci 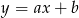 . Podstawiając współrzędne punktów
. Podstawiając współrzędne punktów 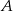 i
i 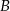 otrzymujemy układ równań
otrzymujemy układ równań
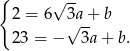
Odejmujemy od pierwszego równania drugie (żeby zredukować 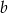 ) i mamy
) i mamy
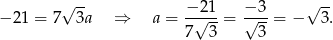
Wtedy 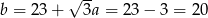 i prosta
i prosta 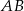 ma równanie
ma równanie 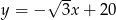 .
.
Dwie półpłaszczyzny o krawędzi 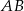 są opisane nierównościami
są opisane nierównościami
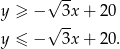
W której z tych półpłaszczyzn znajduje się punkt 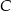 ? – aby to ustalić, wystarczy sprawdzić, którą z powyższych nierówności spełniają jego współrzędne. Liczymy
? – aby to ustalić, wystarczy sprawdzić, którą z powyższych nierówności spełniają jego współrzędne. Liczymy
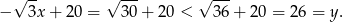
Zatem jest to półpłaszczyzna
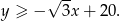
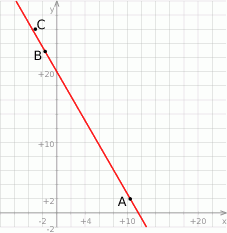
Na koniec obrazek dla ciekawskich
Odpowiedź: