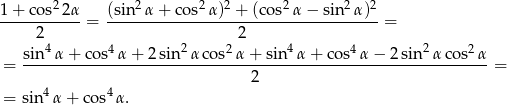Zadanie nr 1221830
Wykaż, że dla dowolnego kąta  prawdziwa jest tożsamość
prawdziwa jest tożsamość 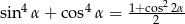 .
.
Rozwiązanie
Sposób I
Przekształcamy lewą stronę tożsamości korzystając z jedynki trygonometrycznej i wzoru na 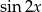 .
.
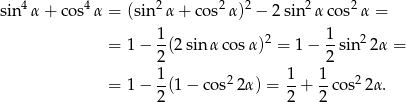
Sposób II
Tym razem przekształćmy prawą stronę korzystając z jedynki trygonometrycznej i wzoru na 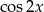 .
.