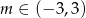Zadanie nr 7174491

Wyznacz wszystkie wartości parametru 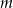, dla których wśród rozwiązań równania

|m − 5x| = 3

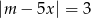
są zarówno liczby dodatnie, jak i ujemne.

Rozwiązanie

Rozwiązujemy dane równanie.

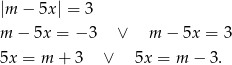
|m − 5x | = 3 m − 5x = − 3 ∨ m − 5x = 3 5x = m + 3 ∨ 5x = m − 3.

Sposób I

Jeżeli jedna z tych liczb ma być ujemna, a druga dodatnia, to musi być spełniony warunek

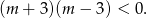
(m + 3 )(m − 3) < 0 .

Jest to zwykła nierówność kwadratowa i jej rozwiązaniem jest przedział 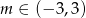m ∈ (− 3,3) .

Sposób II

Ponieważ 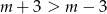m + 3 > m − 3 , to pierwsza z tych liczb musi być dodatnia, a druga ujemna. Mamy stąd

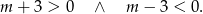
m + 3 > 0 ∧ m − 3 < 0.

Stąd 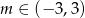m ∈ (− 3,3) .
Odpowiedź: