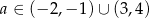/Szkoła średnia/Równania/Z wartością bezwględną

Zadanie nr 8379656

Dodaj do ulubionych
Dodaj do rozwiązanych

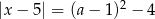Wyznacz wszystkie wartości parametru a , dla których równanie |x − 5| = (a − 1)2 − 4 ma dwa różne rozwiązania dodatnie.

Rozwiązanie

Zapiszmy dane równanie w postaci

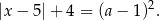
2 |x− 5|+ 4 = (a− 1 ) .

Szkicujemy teraz wykres lewej strony – jest to wykres funkcji 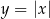y = |x | przesunięty o 5 jednostek w prawo i cztery do góry.

PIC

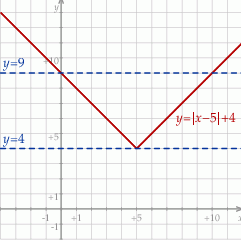
Z wykresu widać, że dane równanie ma dwa rozwiązania dodatnie wtedy i tylko wtedy, gdy prawa strona jest w przedziale 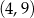(4,9) . Pozostało rozwiązać nierówność

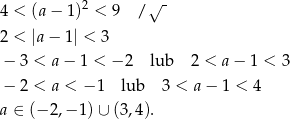
4 < (a − 1)2 < 9 /√ - 2 < |a − 1| < 3 − 3 < a − 1 < − 2 lub 2 < a− 1 < 3 − 2 < a < − 1 lub 3 < a− 1 < 4 a ∈ (− 2,− 1)∪ (3,4).

 
Odpowiedź: a ∈ (− 2,− 1) ∪ (3,4)

Wersja PDF