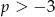Zadanie nr 3979817

Wyznacz te wartości parametru 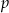, dla których ciąg o wyrazie ogólnym 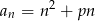an = n2 + pn jest rosnący.

Rozwiązanie

Ciąg jest rosnący jeżeli 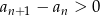an+1 − an > 0 . Mamy zatem nierówność

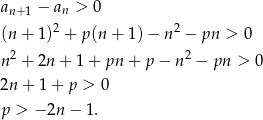
a − a > 0 n+ 1 n (n + 1)2 + p(n + 1 )− n 2 − pn > 0 2 2 n + 2n + 1 + pn + p − n − pn > 0 2n + 1 + p > 0 p > −2n − 1.

Ponieważ 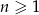n ≥ 1 , to największą (czyli najmniej ujemną) wartością prawej strony jest

− 2⋅1 − 1 = − 3.

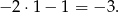
Zatem ciąg 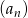(an) jest rosnoący o ile p > − 3 .
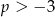Odpowiedź: