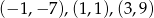/Szkoła średnia/Funkcje - wykresy/Wielomiany/Wyższego stopnia

Zadanie nr 5660470

Dodaj do ulubionych
Dodaj do rozwiązanych

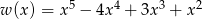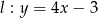Wyznacz punkty wspólne wykresu wielomianu 5 4 3 2 w (x) = x − 4x + 3x + x i prostej l : y = 4x − 3 .

Rozwiązanie

Musimy rozwiązać równanie 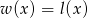w (x) = l(x ) .

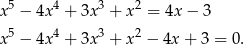
5 4 3 2 x − 4x + 3x + x = 4x − 3 x5 − 4x 4 + 3x 3 + x2 − 4x+ 3 = 0.

Sposób I

Jeżeli się przyjrzymy to widać, że z lewej strony możemy wyłączyć wyrażenie 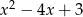x 2 − 4x + 3 .

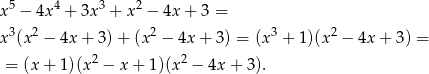
x5 − 4x4 + 3x3 + x2 − 4x + 3 = 3 2 2 3 2 x (x − 4x + 3) + (x − 4x + 3) = (x + 1 )(x − 4x + 3) = = (x+ 1)(x2 − x + 1)(x2 − 4x + 3).

Widać zatem, że jeden z pierwiastków to 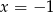x = −1 , drugi nawias jest zawsze dodatni (bo 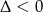Δ < 0 ), pozostało więc rozłożyć trójmian w trzecim nawiasie.

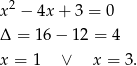
x2 − 4x+ 3 = 0 Δ = 16 − 1 2 = 4 x = 1 ∨ x = 3.

Odpowiadające 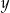y -ki wyliczamy z równania prostej:

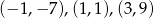
(− 1,− 7),(1,1),(3 ,9)

Sposób II

Szukamy pierwiastków całkowitych wśród dzielników wyrazu wolnego. Znajdujemy bez trudu 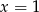x = 1 . Dzielimy wielomian przez 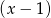(x− 1) . My zrobimy to grupując wyrazy.

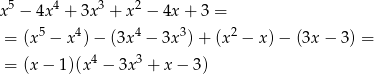
5 4 3 2 x − 4x + 3x + x − 4x+ 3 = = (x 5 − x 4)− (3x 4 − 3x3)+ (x2 − x)− (3x − 3) = 4 3 = (x − 1)(x − 3x + x − 3)

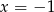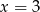Rozkładamy teraz wielomian w nawiasie, łatwo znaleźć jego pierwiastek x = − 1 lub x = 3 . My podzielimy przez x− 3 .

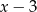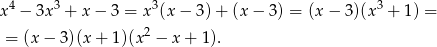
x4 − 3x3 + x − 3 = x3(x− 3)+ (x− 3) = (x − 3)(x3 + 1) = 2 = (x − 3)(x + 1 )(x − x+ 1).

Otrzymany wielomian kwadratowy nie ma pierwiastków (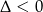Δ < 0 ), więc wszystkie pierwiastki wyjściowego równania, to 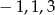− 1,1,3 . Licząc 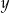y –ki mamy

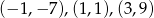
(− 1,− 7),(1,1),(3 ,9)

Na koniec obrazek

PIC

 
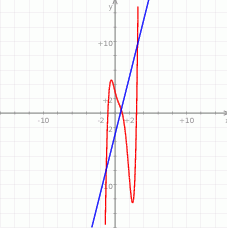
Odpowiedź: (− 1,− 7),(1,1),(3,9 )

Wersja PDF
Rozwiązanie Losuj ponownie