Zadanie nr 4914194
Dany jest prostokąt o wymiarach 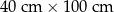 . Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
. Jeżeli każdy z dłuższych boków tego prostokąta wydłużymy o 20%, a każdy z krótszych boków skrócimy o 20%, to w wyniku obu przekształceń pole tego prostokąta
A) zwiększy się o 8% B) zwiększy się o 4%
C) zmniejszy się o 8% D) zmniejszy się o 4%
Rozwiązanie
Sposób I
Boki prostokąta po opisanej zmianie mają długości
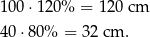
Liczymy jeszcze pole przed i po zmianie.
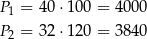
Po zmianach pole zmniejszyło się więc o 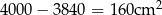 , co stanowi
, co stanowi
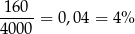
początkowego pola.
Sposób II
Jeżeli oznaczymy długości boków prostokąta przez  i
i 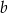 , to po zmianie długości boków otrzymamy prostokąt o bokach długości
, to po zmianie długości boków otrzymamy prostokąt o bokach długości 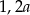 i
i 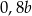 . Jego pole jest więc równe
. Jego pole jest więc równe
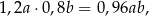
czyli 96% pola pierwszego prostokąta. Pole zmniejszyło się więc o 4%.
Odpowiedź: D

