Zadanie nr 8929805
Prosta przechodząca przez punkty 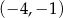 oraz
oraz 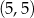 ma równanie
ma równanie
A) 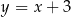 B)
B) 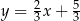 C)
C) 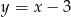 D)
D) 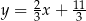
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

