/Szkoła średnia/Zadania maturalne/Matura 2010/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 13 marca 2010 Czas pracy: 180 minut
Wykres funkcji 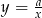 , gdzie
, gdzie 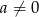 przesunięto o wektor
przesunięto o wektor ![[2,3]](https://img.zadania.info/zes/0080194/HzesT2x.gif) i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu
i otrzymano wykres funkcji, która ma dokładnie dwa punkty wspólne z okręgiem o równaniu 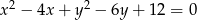 . Wyznacz
. Wyznacz  .
.
W trójkącie o obwodzie 14 jeden z boków jest dwa razy dłuższy od drugiego boku. Oblicz cosinus najmniejszego kąta, tego spośród trójkątów spełniających podany warunek, w którym suma kwadratów długości boków jest najmniejsza.
Rozwiąż nierówność 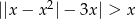 .
.
Oblicz iloczyn pierwszych 99 wyrazów ciągu geometrycznego 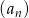 , w którym
, w którym 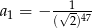 oraz
oraz 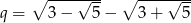 . Czy iloczyn ten jest liczbą wymierną?
. Czy iloczyn ten jest liczbą wymierną?
Zaznacz w układzie współrzędnych zbiór punktów, których współrzędne 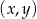 są rozwiązaniem układu nierówności
są rozwiązaniem układu nierówności
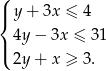
Oblicz pole tego obszaru.
Dane jest równanie 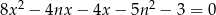 z niewiadomą
z niewiadomą  i parametrem
i parametrem  .
.
- Wyznacz wszystkie wartości
 , dla których suma odwrotności pierwiastków tego równania jest równa
, dla których suma odwrotności pierwiastków tego równania jest równa 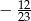 .
. - Wykaż, że jeżeli
 jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
jest liczbą całkowitą, to suma kwadratów pierwiastków tego równania też jest liczbą całkowitą.
W trójkącie 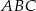 punkt
punkt 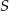 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 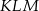 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 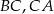 i
i 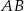 odpowiednio.
odpowiednio.
- Uzasadnij, że na czworokącie
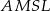 można opisać okrąg.
można opisać okrąg. - Wiedząc, że
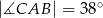 oraz
oraz 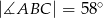 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 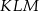 .
.
Do woreczka wrzucono 3 monety 5 złotowe, 4 monety 2 złotowe, 2 monety 1 złotowe oraz 8 monet 50 groszowych. Karol losowo wyjmuje z woreczka 10 monet. Jakie jest prawdopodobieństwo, że wylosuje w ten sposób co najmniej 10 zł? Wynik podaj z dokładnością do trzech miejsc po przecinku.
Podstawą graniastosłupa prostego 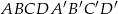 jest równoległobok
jest równoległobok 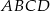 o bokach długości
o bokach długości 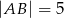 i
i 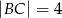 . Oblicz długość wysokości
. Oblicz długość wysokości 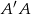 graniastosłupa jeżeli
graniastosłupa jeżeli 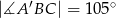 oraz
oraz 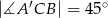 .
.
Rozwiąż równanie 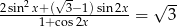 .
.

