/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Losy

Zadanie nr 7033554

W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest wygrywających, jeżeli prawdopodobieństwo wygranej jest równe 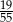19 55 ?

Rozwiązanie

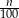Jeżeli oznaczymy przez liczbę losów wygrywających, to prawdopodobieństwo wygranej przy pierwszym losowaniu jest równe n100- , a prawdopodobieństwo wygranej przy drugiej próbie jest równe

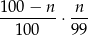
100-−-n-⋅ n-- 100 99

(za pierwszym razem musimy wyciągnąć los przegrywający). Pozostało rozwiązać równanie

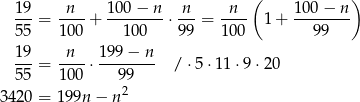
( ) 19- -n-- 100-−-n- -n- -n-- 10-0−--n 55 = 100 + 100 ⋅9 9 = 10 0 1 + 99 19-= -n--⋅ 199−--n- / ⋅5⋅1 1⋅9 ⋅20 55 100 99 342 0 = 199n − n 2

Rozwiązujemy otrzymane równanie kwadratowe.

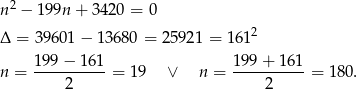
2 n − 199n + 342 0 = 0 Δ = 39 601− 13680 = 25921 = 1612 n = 199-−-1-61 = 19 ∨ n = 1-99+--161 = 1 80. 2 2

Drugą odpowiedź odrzucamy (bo wszystkich losów jest 100) i mamy 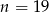n = 19 .
Odpowiedź: Było 19 losów wygrywających.

Rozwiązanie Losuj ponownie