/Szkoła średnia/Zadania testowe/Liczby/Wyrażenia algebraiczne/Wielomianowe

Zadanie nr 6162059

Dodaj do ulubionych
Dodaj do rozwiązanych

Po przekształceniu wyrażenia algebraicznego 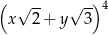( √ -- √ -) 4 x 2 + y 3 do postaci 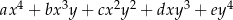4 3 2 2 3 4 ax + bx y+ cx y + dxy + ey współczynnik c jest równy
A) 6 B) 36 C) 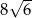√ -- 8 6 D) √ -- 12 6

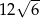
Rozwiązanie

Sposób I

Zauważmy najpierw, że

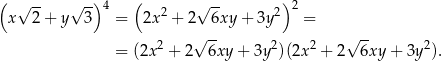
( √ -- √ -) 4 ( √ -- ) 2 x 2 + y 3 = 2x 2 + 2 6xy + 3y2 = √ -- √ -- = (2x2 + 2 6xy + 3y2)(2x2 + 2 6xy + 3y2).

Przy wymnażaniu wyrażeń w tych nawiasach otrzymamy trzy składniki zawierające 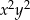2 2 x y :

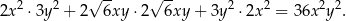
2 2 √ -- √ -- 2 2 2 2 2x ⋅3y + 2 6xy ⋅ 2 6xy + 3y ⋅2x = 36x y .

Sposób II

Korzystamy ze wzoru skróconego mnożenia

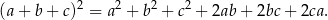
2 2 2 2 (a + b + c) = a + b + c + 2ab+ 2bc+ 2ca.

W naszej sytuacji mamy

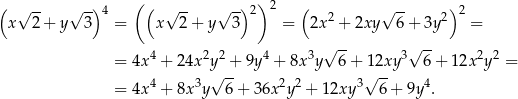
( √ -- √ -) 4 (( √ -- √ -) 2) 2 ( √ -- ) 2 x 2+ y 3 = x 2 + y 3 = 2x 2 + 2xy 6 + 3y2 = √ -- √ -- = 4x4 + 24x2y 2 + 9y 4 + 8x 3y 6 + 12xy 3 6+ 12x2y2 = √ -- √ -- = 4x4 + 8x3y 6 + 3 6x2y2 + 12xy 3 6+ 9y4.

Interesujący nas współczynnik przy 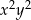2 2 x y jest więc równy 36.

Sposób III

Korzystamy ze wzoru dwumianowego Newtona

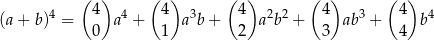
( ) ( ) ( ) ( ) ( ) 4 4 4 4 3 4 2 2 4 3 4 4 (a+ b) = 0 a + 1 a b + 2 a b + 3 ab + 4 b

W takim razie składnik wyrażenia 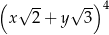( √ -- √ -) 4 x 2 + y 3 zawierający 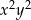2 2 x y jest równy

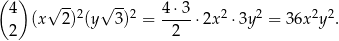
( ) √ -- √ -- 4 (x 2)2(y 3)2 = 4-⋅3 ⋅2x2 ⋅3y2 = 36x 2y2. 2 2

 
Odpowiedź: B

Wersja PDF