Zadanie nr 6146016
Uzasadnij, że jeżeli 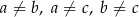 i
i 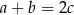 , to
, to 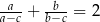 .
.
Rozwiązanie
Sposób I
Zauważmy, że podany warunek możemy zapisać w postaci 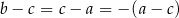 . Zatem
. Zatem
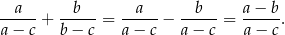
Teraz podstawmy w tej równości 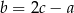
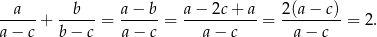
Sposób II
Z podanego warunku mamy 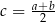 . Zatem
. Zatem
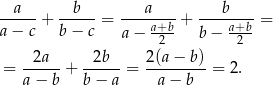
Sposób III
Podstawmy 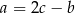 w liczniku i mianowniku pierwszego ułamka.
w liczniku i mianowniku pierwszego ułamka.
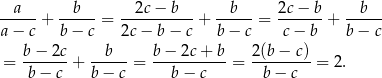
Sposób IV
Przekształćmy w sposób równoważny równość, którą mamy udowodnić.
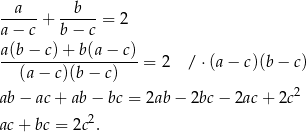
Jeżeli 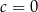 to powyższa równość jest oczywiście spełniona, a jeżeli
to powyższa równość jest oczywiście spełniona, a jeżeli 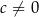 to możemy tę równość podzielić stronami przez
to możemy tę równość podzielić stronami przez  i otrzymujemy prawdziwą równość
i otrzymujemy prawdziwą równość
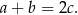
Przekształcaliśmy przy pomocy równoważności, więc wyjściowa równość też musiała być prawdziwa.
Sposób V
Z warunku 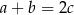 wynika, że liczby
wynika, że liczby 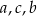 są kolejnymi wyrazami ciągu arytmetycznego. Zatem
są kolejnymi wyrazami ciągu arytmetycznego. Zatem 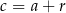 i
i 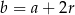 dla pewnego
dla pewnego  . Zatem
. Zatem