Zadanie nr 2685019
Wykaż, że jeżeli 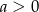 i
i 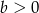 oraz
oraz 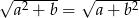 , to
, to 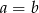 lub
lub 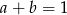 .
.
Rozwiązanie
Przekształcamy równoważnie podaną równość.
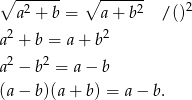
Widać zatem, że równość ta jest spełniona dla 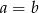 . Załóżmy zatem dalej, że
. Załóżmy zatem dalej, że 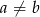 – wtedy możemy ostatnią równość podzielić stronami przez
– wtedy możemy ostatnią równość podzielić stronami przez 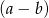 i mamy
i mamy