Zadanie nr 4368082
Ile jest liczb dziewięciocyfrowych, w których suma każdych trzech kolejnych cyfr jest równa 10?
Rozwiązanie
Powiedzmy, że kolejne cztery cyfry liczby, o jakiej mowa w treści zadania to 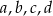 . W takim razie musimy mieć
. W takim razie musimy mieć
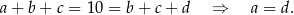
W takim razie cyfry takiej liczby muszą się cyklicznie powtarzać - cyfry 1,4 i 7 muszą być identyczne, podobnie dla cyfr o numerach 2,5,8 i 3,6,9. To oznacza, że liczba musi mieć postać
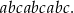
Zauważmy, że w liczbie tej postaci suma dowolnych trzech kolejnych cyfr jest równa 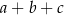 , więc wystarczy zagwarantować, aby
, więc wystarczy zagwarantować, aby 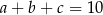 , a wtedy automatycznie liczba ta będzie spełniać warunki zadania.
, a wtedy automatycznie liczba ta będzie spełniać warunki zadania.
Obliczmy na ile sposobów można wybrać cyfry 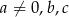 , tak aby
, tak aby 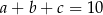 .
.
Sposób I
Oczywiście tylko jedna spośród cyfr 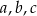 może być równa zero i nie może to być
może być równa zero i nie może to być  . Obliczmy ile jest możliwości z jednym zerem. Liczbę
. Obliczmy ile jest możliwości z jednym zerem. Liczbę  możemy wybrać na 9 sposobów, drugą niezerową liczbę mamy już wyznaczoną jednoznacznie (bo suma ma być równa 10), ale musimy jeszcze ustalić, czy jest to
możemy wybrać na 9 sposobów, drugą niezerową liczbę mamy już wyznaczoną jednoznacznie (bo suma ma być równa 10), ale musimy jeszcze ustalić, czy jest to 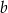 , czy
, czy  . Jest więc
. Jest więc
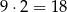
takich liczb.
Dalej załóżmy już, że mamy tylko niezerowe cyfry.
Obliczmy teraz ile jest możliwości z dwoma równymi cyframi (nie mogą być trzy równe cyfry). Są 4 sposoby rozpisania 10-ki w ten sposób:
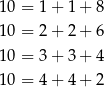
i każdy z tych rozkładów daje 3 możliwe trójki liczb 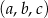 – wystarczy bowiem ustalić, które dwie z liczb
– wystarczy bowiem ustalić, które dwie z liczb 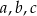 mają być równe i wtedy trzecia liczba jest już jednoznacznie wyznaczona. Jest więc
mają być równe i wtedy trzecia liczba jest już jednoznacznie wyznaczona. Jest więc
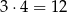
układów z dwoma równymi cyframi.
Pozostało obliczyć liczbę trójek 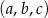 , w których żadne dwie cyfry nie są równe. Możemy 10 rozpisać w ten sposób na 4 sposoby
, w których żadne dwie cyfry nie są równe. Możemy 10 rozpisać w ten sposób na 4 sposoby
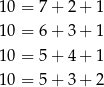
i każdy z tych rozkładów daje 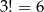 możliwych trójek liczb
możliwych trójek liczb 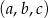 . Są więc
. Są więc
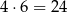
liczby tej postaci.
W sumie są więc
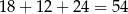
liczby spełniające warunki zadania.
Sposób II
Zauważmy liczba  jest jednoznacznie wyznaczona przez wybór
jest jednoznacznie wyznaczona przez wybór  i
i 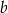 oraz warunek
oraz warunek 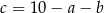 . Wystarczy zatem ustalić na ile sposobów można wybrać
. Wystarczy zatem ustalić na ile sposobów można wybrać  i
i 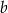 tak, aby
tak, aby 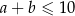 .
.
Jeżeli 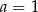 , to
, to 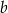 możemy wybrać na 10 sposobów; jeżeli
możemy wybrać na 10 sposobów; jeżeli 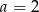 , to
, to 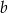 możemy wybrać na 9 sposobów (bo nie może być równe 9), itd. Jeżeli
możemy wybrać na 9 sposobów (bo nie może być równe 9), itd. Jeżeli 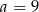 , to
, to 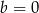 lub
lub 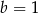 . W sumie są więc
. W sumie są więc
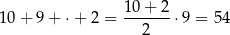
możliwości.
Odpowiedź: 54

