Zadanie nr 2755855
Wyznacz asymptoty funkcji 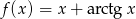 .
.
Rozwiązanie
Funkcja nie ma asymptot pionowych (bo dziedziną jest 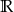 ), więc od razu szukamy asymptoty ukośnej. Po drodze będziemy korzystać z tego, że
), więc od razu szukamy asymptoty ukośnej. Po drodze będziemy korzystać z tego, że
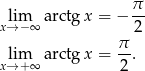
Najpierw asymptota w  .
.
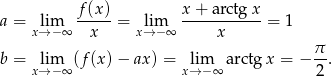
Zatem prosta 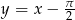 jest asymptotą ukośną w
jest asymptotą ukośną w 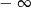 .
.
Teraz asymptota w 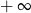 .
.
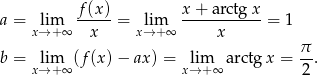
Zatem prosta 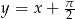 jest asymptotą ukośną w
jest asymptotą ukośną w 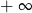 .
.
Na koniec obrazek.
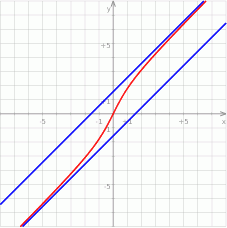
Odpowiedź: 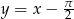 w
w 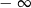 oraz
oraz 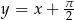 w
w 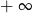 .
.

