/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Liniowy/Dany wykres

Zadanie nr 5578034

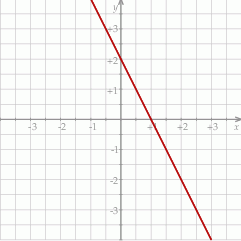
Na rysunku przedstawiono fragment wykresu pewnej funkcji liniowej f .

PIC

Funkcja liniowa 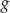g , której wykres jest symetryczny do wykresu funkcji 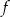f względem poziomej osi układu współrzędnych, jest określona wzorem
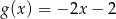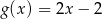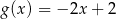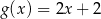
A) g(x ) = − 2x − 2 B) g (x ) = 2x − 2 C) g(x ) = − 2x+ 2 D) g (x ) = 2x + 2

Wersja PDF

Rozwiązanie

Sposób I

Jeżeli odbijemy dany wykres funkcji liniowej względem osi 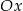Ox , to otrzymamy prostą przechodzącą przez punkty 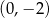(0,− 2) i (1,0) .

PIC

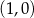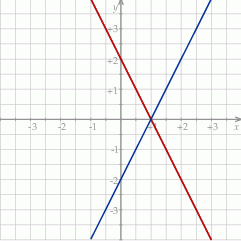
Jest to więc prosta postaci 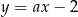y = ax− 2 . Współczynnik a wyznaczamy podstawiając współrzędne punktu (1,0) .

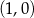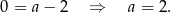
0 = a− 2 ⇒ a = 2.

Odbita prosta ma więc równanie 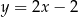y = 2x − 2 .

Sposób II

Dana prosta przechodzi przez punkt 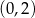(0,2) , więc ma równanie postaci 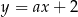y = ax+ 2 . Przechodzi ponadto przez punkt 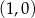(1,0) , więc

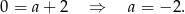
0 = a+ 2 ⇒ a = − 2.

Jest to więc prosta 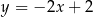y = − 2x + 2 . Prosta symetryczna do niej względem osi 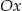Ox ma przeciwny współczynnik kierunkowym, bo tworzy z osią 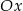Ox kąt skierowany przeciwny do kąta jaki tworzy z osią 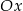Ox pierwsza prosta. Ponadto przecina oś 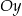Oy w punkcie 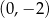(0,− 2) , więc jest to prosta: y = 2x − 2 .  
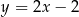Odpowiedź: B

Wersja PDF