/Szkoła średnia/Zadania testowe/Kombinatoryka/Zbiory liczb/Cyfry

Zadanie nr 3115514

Ile jest wszystkich liczb czterocyfrowych, większych 3000, utworzonych wyłącznie z cyfr 1, 2, 3, przy założeniu, że cyfry mogą się powtarzać, ale nie wszystkie z tych cyfr muszą być wykorzystane?
A) 3 B) 6 C) 9 D) 27

Wersja PDF

Rozwiązanie

Sposób I

Skoro liczby mają być większe od 3000, to pierwsza cyfra każdej z takich liczb musi być równa 3. Każdą z pozostałych 3 cyfr możemy wybrać dowolnie spośród liczb: 1, 2, 3. Jest więc

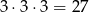
3⋅ 3⋅3 = 27

takich liczb.

Sposób II

Wypisujemy wszystkie liczby spełniające warunki zadania.

3111 , 3112 , 312 1, 32 11, 31 13, 3 131, 3311, 3122, 3212, 3221, 3133 , 3313 , 333 1, 31 23, 31 32, 3 213, 3312, 3231, 3321, 3222, 3223 , 3232 , 332 2, 32 33, 33 23, 3 332, 3333.

 
Odpowiedź: D

Wersja PDF