Zadanie nr 6788058
Oblicz sumę wszystkich liczb dwucyfrowych, które są podzielne przez 4 lub są podzielne przez 6.
Rozwiązanie
Obliczmy najpierw sumę liczb podzielnych przez 4. Liczby te to
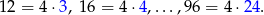
Widać, że liczby te tworzą ciąg arytmetyczny długości 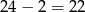 . Zatem ich suma wynosi
. Zatem ich suma wynosi
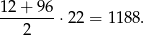
Teraz obliczmy sumę liczb podzielnych przez 6. Liczby te to
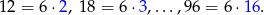
Widać, że liczby te tworzą ciąg arytmetyczny długości 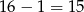 . Zatem ich suma wynosi
. Zatem ich suma wynosi
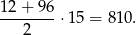
W sumie mamy więc 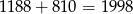 . Jest jednak mały kłopot, bo liczby, które dzielą się jednocześnie przez 4 i przez 6, czyli takie, które dzielą się przez 12, policzyliśmy podwójnie. Sprawdźmy jak jest ich suma. Liczby podzielne przez 12 to
. Jest jednak mały kłopot, bo liczby, które dzielą się jednocześnie przez 4 i przez 6, czyli takie, które dzielą się przez 12, policzyliśmy podwójnie. Sprawdźmy jak jest ich suma. Liczby podzielne przez 12 to
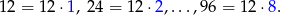
zatem ich suma wynosi
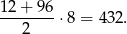
Musimy tę sumę odjąć od wcześniej otrzymanej sumy (bo liczyliśmy te liczby dwa razy). Daje nam to
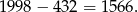
Odpowiedź: 1566

