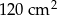Zadanie nr 9758449
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
Rozwiązanie
Zaczynamy oczywiście od rysunku. Od razu narysowaliśmy na nim dwie wysokości trapezu, które okażą się pomocne w rozwiązaniu.
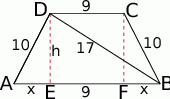
Sposób I
Jeżeli popatrzymy na trójkąty prostokątne 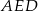 i
i 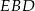 , to w każdym z nich długości boków możemy zapisać przy pomocy dwóch niewiadomych
, to w każdym z nich długości boków możemy zapisać przy pomocy dwóch niewiadomych 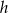 i
i  oraz znanych nam liczb. W takim razie, jeżeli napiszemy twierdzenia Pitagorasa w tych trójkątach, to będziemy mieli dwa równania i dwie niewiadome, czyli w sam raz. Liczymy
oraz znanych nam liczb. W takim razie, jeżeli napiszemy twierdzenia Pitagorasa w tych trójkątach, to będziemy mieli dwa równania i dwie niewiadome, czyli w sam raz. Liczymy
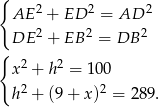
Odejmijmy teraz od drugiego równania pierwsze (żeby skrócić 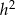 )
)

Stąd 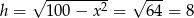 oraz
oraz 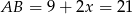 .
.
Mając obie podstawy i wysokość liczymy pole.
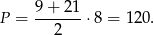
Sposób II
Jeżeli popatrzymy na trójkąt 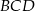 , to mamy dane wszystkie jego boki. Jeżeli mamy wszystkie boki trójkąta, to możemy w nim wyliczyć co tylko chcemy (przynajmniej teoretycznie, bo czasami mogą to być nieprzyjemne rachunki). W szczególności możemy wyliczyć jego wysokość opuszczoną na bok
, to mamy dane wszystkie jego boki. Jeżeli mamy wszystkie boki trójkąta, to możemy w nim wyliczyć co tylko chcemy (przynajmniej teoretycznie, bo czasami mogą to być nieprzyjemne rachunki). W szczególności możemy wyliczyć jego wysokość opuszczoną na bok 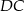 – jest to jednocześnie wysokość trapezu. Jak już będziemy mieli tę wysokość, to z trójkąta
– jest to jednocześnie wysokość trapezu. Jak już będziemy mieli tę wysokość, to z trójkąta 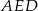 wyliczymy odcinek
wyliczymy odcinek 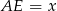 , co da nam długość podstawy
, co da nam długość podstawy 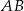 i będziemy mieli pole.
i będziemy mieli pole.
Aby wyliczyć długość wysokości opuszczonej na bok 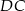 w trójkącie
w trójkącie 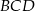 , musimy znać jego pole – a to możemy wyliczyć ze wzoru Herona
, musimy znać jego pole – a to możemy wyliczyć ze wzoru Herona
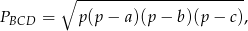
gdzie 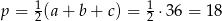 . Zatem
. Zatem
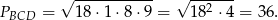
Stąd
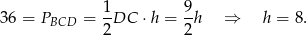
Dalej 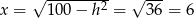 , oraz
, oraz 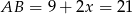 . Pole obliczamy jak w poprzednim sposobie.
. Pole obliczamy jak w poprzednim sposobie.
Odpowiedź: