Zadanie nr 7007519
W trójkącie prostokątnym 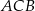 przyprostokątna
przyprostokątna 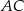 ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta
ma długość 5, a promień okręgu wpisanego w ten trójkąt jest równy 2. Oblicz pole trójkąta 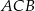 .
.
Rozwiązanie
Szkicujemy trójkąt prostokątny.
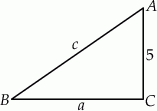
Korzystamy ze wzoru
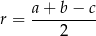
na promień  okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości
okręgu wpisanego w trójkąt prostokątny o przyprostokątnych długości  i
i 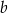 oraz przeciwprostokątnej długości
oraz przeciwprostokątnej długości  . Jeżeli oznaczymy
. Jeżeli oznaczymy 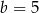 , to mamy
, to mamy
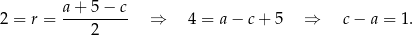
Ponadto, na mocy twierdzenia Pitagorasa
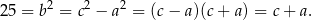
Mamy zatem
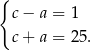
Jeżeli teraz odejmiemy od drugiego równania pierwsze (żeby skrócić  ), to mamy
), to mamy
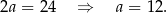
Pole trójkąta 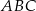 jest więc równe
jest więc równe
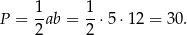
Odpowiedź: 30

