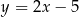Zadanie nr 3967426

Okrąg o środku 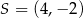S = (4,− 2) przechodzi przez punkt 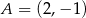A = (2 ,− 1 ) . Napisz równanie stycznej do tego okręgu przechodzącej przez punkt .

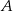Rozwiązanie

Naszkicujmy opisaną sytuację.

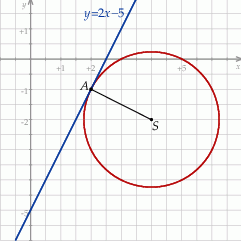
Napiszmy najpierw równanie prostej zawierającej promień 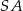. Szukamy prostej w postaci 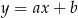y = ax + b i podstawiamy współrzędne punktów 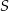i .

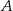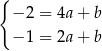
{ − 2 = 4a+ b − 1 = 2a+ b

Odejmujemy od pierwszego równania drugie i mamy

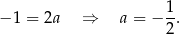
− 1 = 2a ⇒ a = − 1. 2

Współczynnika 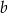możemy nie wyznaczać, bo nie jest nam potrzebny.

Szukana styczna jest prostopadła do promienia 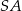, więc ma równanie postaci 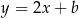y = 2x + b . Współczynnik 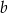wyznaczamy podstawiając współrzędne punktu .

− 1 = 2 ⋅2+ b ⇒ b = − 5.

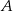Szukana styczna ma więc równanie 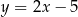y = 2x − 5 .
Odpowiedź: y = 2x− 5