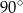Zadanie nr 4835224
Oblicz miarę kąta między stycznymi do okręgu  poprowadzonymi przez punkt
poprowadzonymi przez punkt 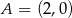 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
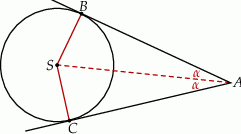
Jeżeli zapiszemy równanie okręgu w postaci
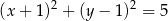
to widać, że mamy do czynienia z okręgiem o środku 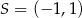 i promieniu
i promieniu 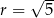 .
.
Sposób I
Jeżeli oznaczymy przez 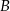 i
i 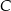 punkty styczności stycznych poprowadzonych z punktu
punkty styczności stycznych poprowadzonych z punktu 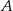 do okręgu, to
do okręgu, to
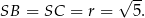
Ponadto
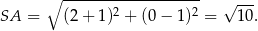
Zatem
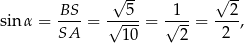
czyli 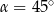 . to oznacza, że
. to oznacza, że 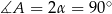 .
.
Sposób II
Tym razem użyjemy odrobinę więcej geometrii analitycznej i wyliczymy równania stycznych.
Proste przechodzące przez punkt 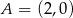 mają postać
mają postać 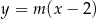 (tak naprawdę brakuje w tym pęku pionowej prostej
(tak naprawdę brakuje w tym pęku pionowej prostej 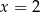 , ale łatwo sprawdzić, że nie jest ona szukaną styczną). Sprawdźmy, kiedy prosta tej postaci jest styczna do okręgu: wstawiamy do równania okręgu
, ale łatwo sprawdzić, że nie jest ona szukaną styczną). Sprawdźmy, kiedy prosta tej postaci jest styczna do okręgu: wstawiamy do równania okręgu 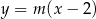 i sprawdzamy, kiedy otrzymane równanie kwadratowe ma dokładnie jeden pierwiastek.
i sprawdzamy, kiedy otrzymane równanie kwadratowe ma dokładnie jeden pierwiastek.
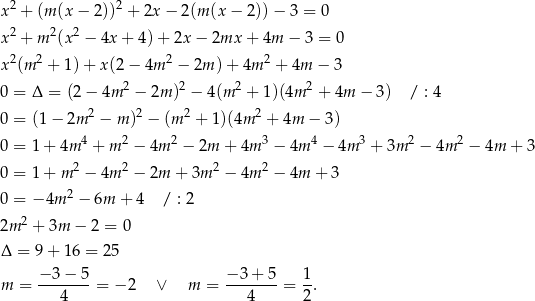
Zatem styczne do okręgu przechodzące przez punkt 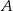 mają postać
mają postać 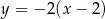 i
i 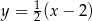 . Teraz wystarczy zauważyć, że iloczyn współczynników kierunkowych tych prostych jest równy -1, więc proste te są prostopadłe.
. Teraz wystarczy zauważyć, że iloczyn współczynników kierunkowych tych prostych jest równy -1, więc proste te są prostopadłe.
Sposób III
Tak jak w poprzednim sposobie szukamy prostej przechodzącej przez punkt 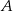 w postaci
w postaci
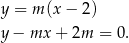
Prosta te będzie styczna do danego okręgu jeżeli odległość środka 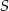 tego okręgu od tej prostej będzie równa
tego okręgu od tej prostej będzie równa 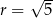 . Na mocy wzoru na odległość punktu od prostej mamy więc równanie
. Na mocy wzoru na odległość punktu od prostej mamy więc równanie
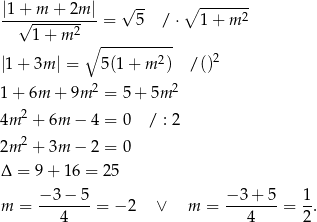
Teraz wystarczy zauważyć, że iloczyn współczynników kierunkowych otrzymanych prostych jest równy -1, więc proste te są prostopadłe.
Na koniec obrazek dla ciekawskich.
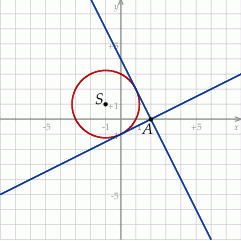
Odpowiedź: