Zadanie nr 4792865
Wykaż, że dla każdej liczby rzeczywistej 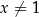 i dla każdej liczby rzeczywistej
i dla każdej liczby rzeczywistej 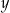 prawdziwa jest nierówność
prawdziwa jest nierówność
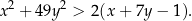
Rozwiązanie
Sposób I
Przekształcamy daną nierówność w sposób równoważny,
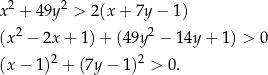
Oczywiście nierówność ta jest spełniona (bo 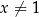 ), a przekształcaliśmy ją w sposób równoważny, więc wyjściowa nierówność też musiała być spełniona.
), a przekształcaliśmy ją w sposób równoważny, więc wyjściowa nierówność też musiała być spełniona.
Sposób II
Traktujemy nierówność, którą mamy udowodnić
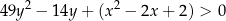
jak zwykłą nierówność kwadratową z niewiadomą 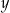 i parametrem
i parametrem  . Liczymy
. Liczymy 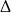 –ę.
–ę.
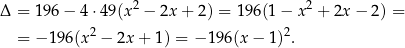
Ponieważ 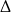 jest ujemna (bo
jest ujemna (bo 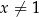 ), powyższa nierówność jest zawsze spełniona (bo parabola będąca wykresem lewej strony jest powyżej osi
), powyższa nierówność jest zawsze spełniona (bo parabola będąca wykresem lewej strony jest powyżej osi 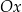 ).
).

