/Szkoła średnia/Nierówności/Udowodnij...

Zadanie nr 4958018

Dodaj do ulubionych
Dodaj do rozwiązanych

Wykaż, że dla dowolnych liczb rzeczywistych 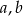a,b spełniona jest nierówność

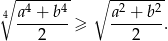
∘ -4----4- ∘ -2----2- 4 a-+--b- ≥ a-+--b-. 2 2

Rozwiązanie

Obie strony nierówności są dodatnie, więc możemy nierówność podnieść stronami do potęgi czwartej i otrzymamy nierówność równoważną.

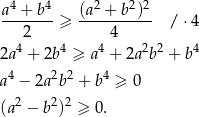
4 4 2 2 2 a-+-b--≥ (a--+-b-)- / ⋅4 2 4 2a 4 + 2b 4 ≥ a4 + 2a 2b2 + b4 a4 − 2a2b2 + b4 ≥ 0 2 2 2 (a − b ) ≥ 0.

Otrzymana nierówność jest oczywiście spełniona, a przekształcaliśmy przy pomocy równoważności, więc wyjściowa nierówność też musi być spełniona.

Wersja PDF