/Szkoła średnia/Funkcje - wykresy/Wartość bezwzględna/Z wykładniczą

Zadanie nr 6754960

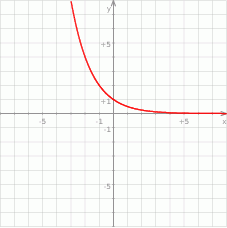
Na rysunku przedstawiono fragment wykresu funkcji wykładniczej określonej wzorem 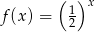( )x f(x ) = 1 2 . Rozważamy funkcję 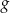g określoną wzorem 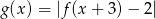g (x ) = |f(x + 3) − 2| . Wyznacz wszystkie wartości parametru 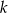k , dla których równanie 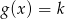g (x) = k ma dwa rozwiązania takie, że ich iloczyn jest liczbą ujemną.

PIC

Wersja PDF

Rozwiązanie

Szkicujemy najpierw wykres funkcji 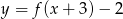y = f(x + 3) − 2 . Wykres ten powstaje z wykresu funkcji 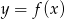y = f (x) przez przesunięcie o 3 jednostki w lewo i dwie w dół (czyli o wektor [− 3,− 2] ).

PIC

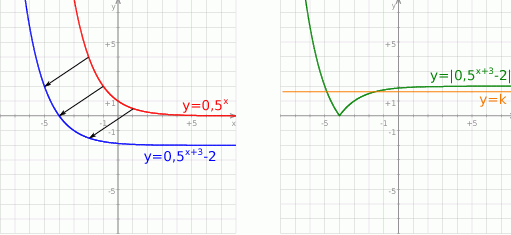
Wykres funkcji 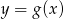y = g(x) otrzymujemy z wykresu 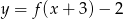y = f (x+ 3)− 2 przez odbicie części znajdującej się pod osią 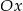Ox do góry.

Sprawdźmy jeszcze gdzie dokładnie wykres 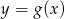y = g(x) przecina oś Oy .

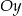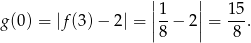
| | |1 | 15 g(0) = |f(3 )− 2| = ||--− 2|| = --. 8 8

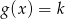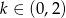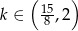Z wykresu widać, że równanie g(x) = k ma dwa pierwiastki jeżeli k ∈ (0,2) . Ponadto pierwiastki te będą miały różne znaki, gdy ( ) k ∈ 15,2 8 .  
Odpowiedź: ( 15 ) k ∈ 8 ,2

Wersja PDF