/Szkoła średnia/Geometria/Planimetria/Trójkąt/Prostokątny/Udowodnij...

Zadanie nr 2471654

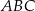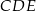Trójkąty prostokątne równoramienne ABC i CDE są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 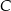C jest prosty). Wykaż, że |AD | = |BE | .

PIC

Wersja PDF

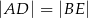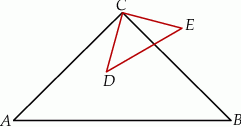
Rozwiązanie

Dorysujmy odcinki 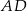AD i BE .

PIC

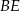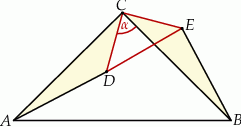
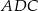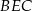Patrzymy teraz na trójkąty ADC i BEC . Mają one dwie pary równych boków

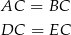
AC = BC DC = EC

oraz równy kąt przy wierzchołku 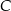C

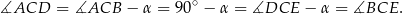
∘ ∡ACD = ∡ACB − α = 90 − α = ∡DCE − α = ∡BCE .

Trójkąty te są więc przystające, czyli 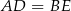AD = BE .

Wersja PDF