/Szkoła podstawowa/Zadania testowe

Zadanie nr 6441176

Dodaj do ulubionych
Dodaj do rozwiązanych

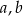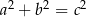Trójki liczb naturalnych a,b i c , które spełniają warunek a2 + b2 = c2 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:

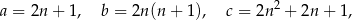
a = 2n + 1, b = 2n(n + 1), c = 2n2 + 2n + 1,

gdzie n oznacza dowolną liczbę naturalną (n ≥ 1 ).
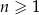Jeżeli najmniejsza z liczb 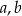a,b i c jest równa 9, to największa z tych liczb jest równa
A) 41 B) 73 C) 145 D) 181

Rozwiązanie

Wśród podanych liczb na najmniejsza to a , więc

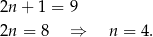
2n + 1 = 9 2n = 8 ⇒ n = 4.

W takim razie największa z liczb jest równa

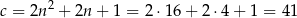
c = 2n2 + 2n + 1 = 2 ⋅16 + 2 ⋅4 + 1 = 41

 
Odpowiedź: A

Wersja PDF