Zadanie nr 5961154
Podstawą graniastosłupa prostego o objętości 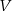 jest równoległobok o bokach długości
jest równoległobok o bokach długości  i
i 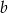 . Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż
. Wykaż, że pole powierzchni bocznej tego graniastosłupa jest nie mniejsze niż 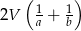 .
.
Rozwiązanie
Oznaczmy przez 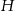 długość wysokości graniastosłupa, a przez
długość wysokości graniastosłupa, a przez  kąt ostry równoległoboku.
kąt ostry równoległoboku.
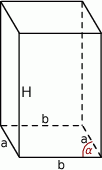
Na mocy wzoru na pole równoległoboku z sinusem, pole podstawy jest równe
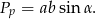
Z podanej objętości mamy więc
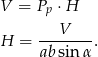
Pole powierzchni bocznej jest więc równe
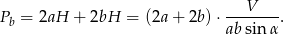
Ponieważ 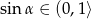 , mamy stąd
, mamy stąd