Zadanie nr 9913009
Dany jest okrąg o promieniu 11 oraz punkt 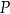 oddalony o 7 od środka okręgu. Przez punkt
oddalony o 7 od środka okręgu. Przez punkt 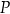 poprowadzono cięciwę o długości 18. W jakim stosunku punkt
poprowadzono cięciwę o długości 18. W jakim stosunku punkt 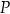 podzielił tę cięciwę na dwa odcinki?
podzielił tę cięciwę na dwa odcinki?
Rozwiązanie
Szkicujemy opisaną sytuację.
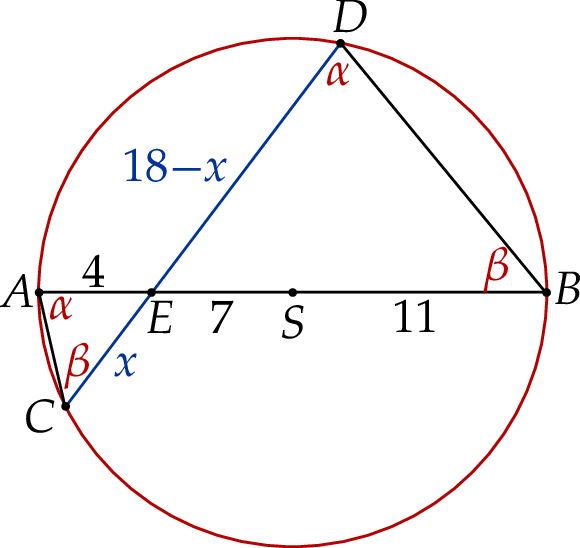
Jeżeli oznaczymy 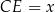 , to
, to 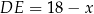 .
.
Sposób I
Korzystamy z twierdzenia o siecznych okręgu.
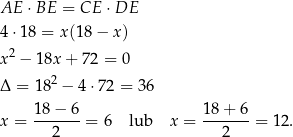
Mamy wtedy odpowiednio 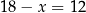 lub
lub 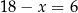 . Stosunek podziału jest więc równy 2 lub
. Stosunek podziału jest więc równy 2 lub 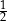 .
.
Sposób II
Zauważmy, że 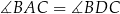 oraz
oraz 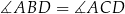 (kąty wpisane oparte na tych samych łukach). To oznacza, że trójkąty
(kąty wpisane oparte na tych samych łukach). To oznacza, że trójkąty 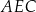 i
i 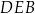 są podobne. W szczególności
są podobne. W szczególności
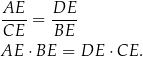
Dalszą część rozwiązania przeprowadzamy dokładnie tak samo jak w pierwszym sposobie.
Odpowiedź: 2 lub 

